Ejercicios Selectividad Junio 2013
Enunciado	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
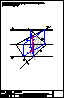
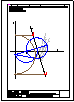
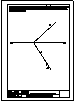
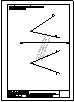
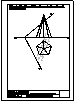
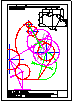
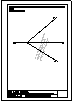
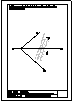
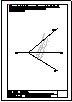
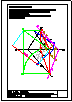
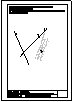
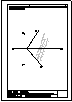
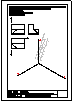
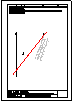
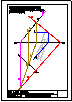
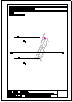
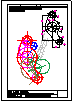
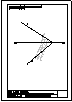
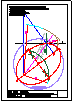
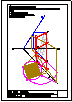
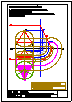
1.- En el punto P se produce el lanzamiento de un proyectil que sigue una trayectoria parabólica. Se        conocen el eje e y la tangente t en ese punto inicial P. Obtener el foco y el punto más alto de la        trayectoria.
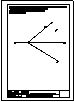
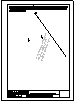
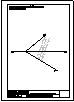
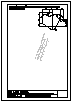
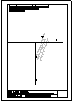
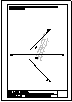
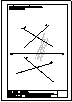
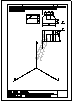
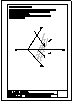
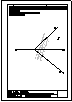
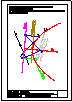
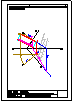
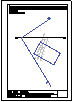
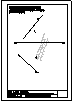
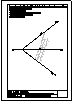
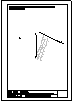
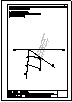
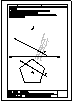
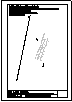
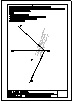
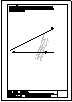
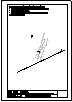
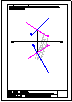
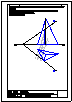
2.- Dadas la recta r y el punto P, determinar la distancia entre ambos.
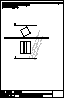
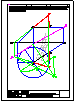
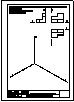
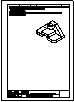
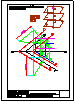
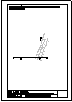
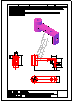
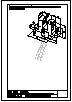
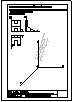
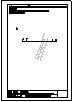
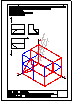
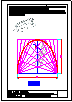
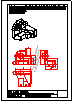
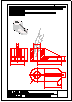
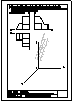
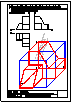
3.- Dibujar las vistas en diédrico (sistema europeo) de planta, alzado y perfil. Dibujar una perspectiva        de la pieza desde un punto de vista diferente al dado. Aplicar una escala conveniente, deduciendo        distancias directamente del dibujo dado y manteniendo las proporciones.
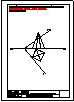
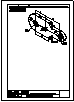
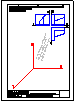
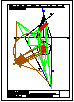
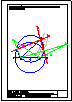
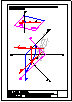
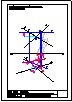
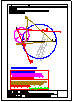
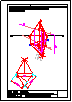
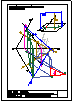
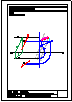
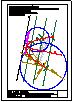
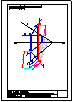
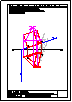
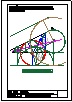
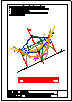
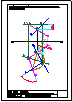
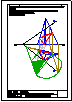
4.- Hallar los 2 puntos de intersección de la recta y la pirámide dadas y visualizar la verdadera        magnitud de la distancia entre ambos puntos.
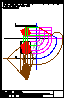
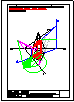
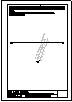
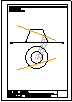
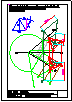
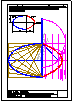
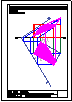
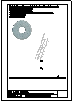
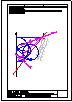
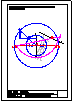
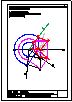
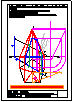
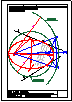
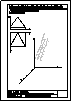
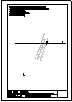
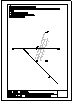
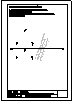
5.- Dado el cono representado en la figura y el plano alpha definido por sus trazas en P-H. y en        P.V., hallar la sección producida por dicho plano sobre el cono, en proyección horizontal, vertical        y en verdadera magnitud.
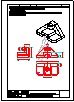
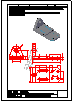
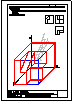
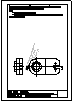
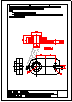
6.- Dada la perspectiva axonométrica de una pieza, dibujar las vistas diédricas necesarias, tomando        directamente las medidas del dibujo y considerando que no se han aplicado coeficientes        de reducción. Acotar según normas UNE.
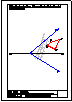
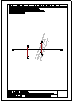
1.- Determinar la directriz y el eje de la parábola cuyo foco es F y que es tangente a la recta r en        el punto T.
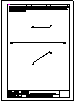
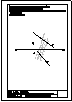
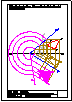
2.- Hallar la distancia entre los dos planos paralelos dados.
3.- Dados la planta y el alzado de una pieza en diédrico (sistema europeo), dibujar el perfil izquierdo        con aristas vistas y ocultas si las hubiera y hacer una perspectiva de la pieza completa a mano        alzada.
4.- Dada la perspectiva axonométrica de una pieza, representar la perspectiva caballera de la misma        sobre el sistema de ejes dado, sin aplicar coeficientes de reducción. Tomad medidas directamente en        el dibujo y considerar que en la isometría no se han aplicado coeficientes de reducción.        Representar aristas vistas y ocultas.
5.- Un plano está definido por las rectas r y s. Determinar la trayectoria seguida por una gota        de agua, situada en unpunto P del plano, dada su proyección horizontal.
6.- Hallar el desarrollo lateral de una pirámide pentagonal regular afectada por un plano        proyectante vertical.

Ejercicios Selectividad JuLio 2013
Enunciado	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Dadas las vistas de planta y alzado de una pieza, dibujar la vista de perfil tomando medidas        directamente del dibujo propuesto. Realiza una perspectiva de dicha pieza a mano alzada.
2.- Dibuja a escala 1:1 la figura propuesta, sin borrar las construcciones auxiliares necesarias y        marcando los puntos de tangencia.
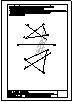
3.- Dada la proyección vertical de un triángulo contenido en el plano P, hallar:        - la proyección horizontal de dicho triángulo.        - la verdadera magnitud del triángulo        - las proyecciones horizontal y vertical del incentro de dicho triángulo
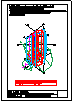
4.- Los puntos A y B definen una arista de un tetraedro regular. El vértice C está en el plano        horizontal. Representar el cuerpo en el primer diedro.
5.- Dadas las proyecciones diédricas de una pieza a escala 1:1, dibujar a escala 3:2        la PERSPECTIVA ISOMÉTRICA tomando medidas directamente del dibujo y sin aplicar        coeficiente de reducción. Respetad el sistema de ejes propuesto.
6.- Dados el plano alpha y la base ABCD de una pirámide regular de altura 40 mm apoyada en        el P.H., determinar:        - la proyección vertival de la pirámide.        - las proyecciones horizontal y vertical que produce el plano alpha sobre la pirámide.        - verdadera magnitud de dicha sección.
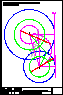
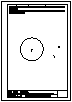
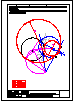
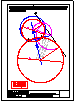
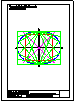
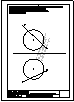
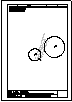
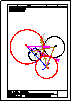
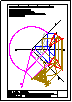
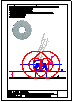
1.- Dibujar las 2 circunferencias tangentes a la recta r y a la circunferencia C, dado el punto de        tangencia P. Dibujar una circunferencia tangente a la recta s y a la circunferencia C.
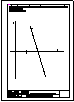
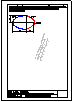
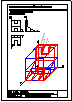
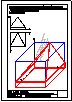
2.- Determinar los 2 puntos de intersección de la recta r con el cubo de lado 40 mm, apoyado        en el plano horizontal. Visualizar la distancia en verdadera magnitud entre ambos puntos.
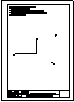
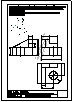
3.- Dados la planta y el perfil izquierdo de una pieza en diédrico (sistema europeo), dibujar la        vista de alzado con aristas vistas y ocultas si las hubiera y hacer una perspectiva de la        pieza a mano alzada.
4.- Representar un tetraedroregular que tiene 400 mm de arista. La cara A, B, C está apoyada        en el plano horizontal. La arista A, B forma 15º con la línea de tierra y el vértice C pertenece        al primer cuadrante. Hallar:        - la proyección horizontal y vertical del tetraedro.        - Si M es el punto medio de la arista AC, determinar las trazas del plano que pasando por M        produce como sección al tetraedro un triángulo equilátero.
5.- Dadas las vistas en diédrico de una pieza, dibujar la perspectiva isométrica de la misma a        escala 4:5 y sin considerar coeficientes de reducción. Representar las aristas vistas y ocultas.
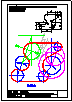
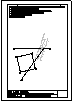
6.- Dada la pirámide pentagonal regular, hallar:        - el ángulo que forma la arista EV con el plano horizontal de proyección.        - los puntos de intersección de la recta r, con la pirámide.        - la distancia en verdadera magnitud entre dichos puntos.

Ejercicios Selectividad Junio 2014
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Dibujar las rectas tangentes a una elipse cuyos ejes miden 10 y 8 cm, desde un punto exterior        situado en la prolongación del eje mayor y a 5cm del foco.
2.- Dadas las rectas "r" y "s" por sus proyecciones diédricas, hallar las trazas del plano que contiene        a la recta "r" y es paralelo a la recta "s".
3.- Se nos da una pieza en perspectiva isométrica dibujada a escala 1: 2, sin aplicar coeficientes de        reducción. Dibujar las vistas diédricas de planta, alzado y perfil de la pieza a escala 1 : 1, tomando        medidas directamente del dibujo. Dibujar aristas vistas y ocultas.
4.- La figura representa la proyección horizontal de un octaedro cuyo vértice inferior está apoyado        sobre el plano horizontal. Obtener la sección que le produce un plano horizontal de cota 30 mm.
5.- Dibujar a escala 2 : 1 la perspectiva isométrica del sólido representado por sus vistas de        planta, alzado y perfil. Tomad medidas directamente del dibujo dado, aplicando coeficientes        de reducción = 1.
6.- Dado el prisma recto de base hexagonal, hallar la sección producida por el plano oblícuo P y su        verdadera magnitud.
1.- Dibujar a escala 1 : 1000 el croquis de la parcela que se adjunta, definida por los vértices A, B, C y       D. Las cotas están expresadas en metros.
2.- Hallar el plano perpendicular al segmento AB, que equidiste de ambos puntos A y B.
3.- Dada la perspectiva isométrica de una pieza a escala 2 : 3, en la que no se han aplicado coeficientes       de reducción, dibujar a escala 1 : 1 las vistas diédricas de planta, alzado y perfil derecho       (método del primer diedro). Aristas vistas y ocultas.
4.- Hallar la sección producida por el plano alpha sobre la pirámide representada y su verdadera       magnitud.
5.- Representar la perspectiva isométrica a escala 2 : 1, tomando medidas directamente de las       vistas dadas y sin aplicar coeficientes de reducción. Representar aristas vistas y ocultas.
6.- Dadas las proyecciones horizontal y vertical de la recta r y de la arista lateral VA de una       pirámide regular de base hexagonal apoyada en el plano horizontal de proyección. Hallar:       - las proyecciones horizontal y vertical de la pirámide.       - los puntos de intersección de la recta r con la pirámide.       - la distancia en verdadera magnitud entre dichos puntos.

Ejercicios Selectividad Julio 2014
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Dada la perspectiva isométrica de una pieza, en la que no se han aplicado coeficientes de        reducción, dibujar las vistas de planta, alzado y perfil a escala 1 : 1 en el sistema europeo,        tomando medidas directamente del dibujo.        A mano alzada, realizar una perspectiva caballera definiendo, sólo aristas vistas.
2.- Hallar las 3 proyecciones diédricas principales de la intersección del cono y la recta dada.
3.- Dibujar a escala 3 : 2, señalando los centros y los puntos de tangencia (indicando las        construcciones auxiliares empleadas).
4.- AB es el lado de un cuadrado situado en el plano alpha. Dibujar las proyecciones horizontal y        vertical de dicho cuadrado.
5.- Dadas las vistas diédricas de planta y alzado de una pieza, dibujadas a escala 1 : 2, representar        la perspectiva caballera de dicha pieza a igual escala, sin aplicar coeficientes de reducción y        respetando el sistema de ejes propuesto.        Es suficiente con dibujar las aristas vistas.
6.- Realizar la perspectiva cónica oblícua del modelo representado, a escala 1 : 1, V se encuentra        situado a 100 mm del plano del cuadro y a 80 mm del plano geometral, en el cual se apoya.        Representar sólo aristas vistas.        Si consideras que puedes tener problemas de espacio, puedes hacer la perspectiva a        escala 1 : 2 ó 2 : 3
1.- Dibujar la vista lateral derecha de la pieza dada.        A mano alzada, realizar una perspectiva cualquiera de la pieza.
2.- Hallar los puntos de intersección de la recta "r" con la pirámide hexagonal regular        de vértice V.
3.- Dibujar a escala 1 : 1 la figura propuesta, dejando indicadas las construcciones        auxiliares empleadas.        En la elipse, intercalar 3 puntos entre dos vértices consecutivos. Los radios de        redondeo no indicados son de 8 mm.
4.- Dibujadas las vistas diédricas de planta y perfil derecho de una pieza a escala 1 : 2, dibujar        la vista de alzado, aplicar los cortes que creas convenientes y acotar.
5.- Dadas las vistas diédricas de planta, alzado y perfil izquierdo (método del primer diedro),        dibujar la perspectiva caballera a escala 1 : 1, sin aplicar coeficientes de reducción. Dibujar        sólo aristas vistas.
6.- Hallar la perspectiva cónica de la pieza representada. El punto de vista está a 85 mm. del        cuadro y a 45 mm. del plano objetivo, en el cual se apoya el modelo. Tomar medidas        directamente sobre el modelo.

Ejercicios Selectividad Junio 2015
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Dibujar el vértice y 6 puntos de una parábola, dados el foco y la directriz.        Trazar la recta tangente a la parábola que pase por el punto P.
2.- Hallar la intersección de la recta y el plano dados.
3.- Dada la perspectiva isométrica de un cuerpo, croquizar las proyecciones diédricas        de planta, alzado y perfil derecho (Sistema Europeo). Incluir aristas ocultas.
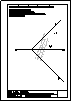
4.- Hallar la verdadera magnitud del ángulo que forman las rectas r y s.
5.- Dadas las proyecciones de planta, alzado y perfil izquierdo de un cuerpo a        escala 1 : 1, dibujar a escala 2 : 1 la proyección isométrica de acuerdo con        los ejes propuestos. Incluir aristas ocultas.
6.- Dibujar la perspectiva cónica de la construcción representada. Aplicar a la        perspectiva una escala 2 : 1, tomando medidas directamente del dibujo dado        (escala 1 : 1). No incluir aristas ocultas.
1.- Dados el eje mayor y menor de una elipse y el punto P, dibujar las tangentes a        dicha elipse desde P.
2.- Dibujar las proyecciones de un tetraedro regular apoyado en el plano horizontal        de proyección. AB es la proyección de una arista horizontal del tetraedro y todo él        se halla en el primer diedro. Hallar los puntos de intersección de la recta r con las        caras del tetraedro.
3.- Hallar la distancia en verdadera magnitud del punto A al plano P dados.
4.- Dadas las proyecciones de planta, alzado y perfil izquierdo de un cuerpo a        escala 1 : 1, dibujar a escala 2 : 1 la perspectiva isométrica, de acuerdo con        los ejes propuestos y sin aplicar coeficientes de reducción. Incluir aristas ocultas.
5.- Dadas las proyecciones horizontal y vertical de un sólido, hallar la sección        producida por el plano P y su verdadera magnitud.
6.- Dadas las trazas del plano P y las proyecciones de la recta r y del punto a, se pide:        - Dibujar las trazas del plano Q, paralelo al plano P y que pase por el punto a.        - Determinar los puntos b y c de intersección de la recta r con los planos P y Q.        - Representar la verdadera magnitud del segmento bc.

Ejercicios Selectividad Julio 2015
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- El segmento AB representa la proyección horizontal de una portería de fútbol.        Los segmentos CD, DE y EF delimitan el área grande de dicho campo. Hallar dos        puntos del segmento DE que generen un ángulo de tiro sobre la portería de        30 grados sexagesimales.        Este problema se debe resolver aplicando el concepto geométrico de Arco Capaz.
2.- Hallar la intersección entre los planos P y R.
3.- Dada la perspectiva isométrica de una pieza croquizar las vistas diédricas de        planta, alzado y perfil derecho, indicando aristas vistas y ocultas.        (Sistema Europeo).
4.- El segmento AB es el lado de un cuadrado situado en el plano a. Dibujar las        proyecciones horizontal y vertical de dicho cuadrado.
5.- Dadas las proyecciones diédricas de una pieza, a escala 1 : 2, representarla        en perspectiva caballera a escala 1 : 1, sin aplicar el coeficiente de reducción        y respetando el sistema de ejes propuesto. Dibujar las aristas vistas y ocultas.
6.- Dadas las proyecciones diédricas de un cuerpo. Representar la perspectiva        cónica oblícua, sabiendo que el punto de vista (V) está situado a 70 mm del        plano del cuadro y a 90 mm del plano geometral, en el cual se apoya.        Escala 1 : 1. No dibujar las aristas ocultas.
1.- Empalmar dos rectas paralelas, r y s, por sus puntos extremos A y B, mediante         dos arcos de circunferencia tangentes entre sí y a dichas rectas, de curvatura         invertida y radios iguales.
2.- Dada la recta ry el punto A, dibujar las trazas del plano que pasa por dicho        punto y es perpendicular a la recta r.
3.- Dada la perspectiva del cuerpo de la figura, croquizar las vistas de alzado,        planta y perfil izquierdo de la pieza representada en sistema axonométrico        isométrico. Incluir aristas ocultas.
4.- Dadas las proyecciones de planta y perfil derecho de una pieza a escala 1 : 2,        dibujar la proyección de alzado aplicando un corte por el plano de simetría.        Acotar la pieza.
5.- A partir de las proyecciones diédricas, dibujar la perspectiva caballera a        escala 1 : 2 con el corte indicado, sin aplicar coeficiente de reducción y sin        incluir aristas ocultas. El eje de revolución de la pieza se hará coincidir con         el eje y.
6.- Hallar la perspectiva cónica de la pieza representada por sus proyecciones        diédricas. El punto de vista está situado a 80 mm del cuadro y a 45 mm del        plano objetivo en el cual se apoya el modelo. Tomar medidas directamente        del modelo y dibujar a escala 1 : 1.

Ejercicios Selectividad Junio 2016
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Localizar un punto P interior al triángulo ABC, que equidiste de los lados AC y BC, y de        forma que el ángulo APB sea de 120º.        Resolverlo aplicando el concepto de Arco Capaz.
2.- Hallar la intersección de los tres planos de la figura, dados por sus trazas horizontal y vertical.
3.- Dibujar a mano alzada las proyecciones ortogonales (planta, alzado y vista lateral izquierda)        de la pieza indicada, sin tomar medidas, pero manteniendo lo más posible las proporciones.
4.- Construir el tetraedro regular, dada su base A´- B´ - C´, en el PH. Determinar en las        proyecciones y en verdadera magnitud, las secciones que producen en el tetraedro los        planos a y b.
5.- Dadas las vistas de una pieza, en proyecciones diédricas. Dibujar, en las tres        proyecciones, un hexágono regular de 15 mm de lado, apoyado en el plano inclinado a        (de trazas ha, va) y con centro en el punto C1.
6.- Dibujar a escala 1 : 1 la planta superior y el alzado cortado por el plano de simetría de        la pieza. Acota        Notas aclaratorias: Utilizar el Sistema Europeo de Proyecciones Diédricas.        Todos los agujeros son pasantes. La pieza tiene dos planos de simetría.        El alzado viene indicado por la letra A y la planta superior por la letra P.
1.- Construir, aplicando el concepto de arco capaz, los 4 triángulos que cumplen las        siguientes condiciones:        - Un lado mide 50 mm y su ángulo opuesto 45º sexagesimales.        - Otro lado mide 65 mm.
2.- Calcular gráficamente la distancia en verdadera magnitud, existente entre el        punto A dado por sus proyecciones, vertical ( A´) y horizontal ( A ) y, el plano        P dado por sus trazas, vertical ( P´ ) y horizontal ( P ).
3.- Dibujar a mano alzada, las proyecciones diédricas (alzado, planta y perfil izquierdo)        en el Sistema Europeo,de la pieza dada por su perspectiva isométrica.        Nota aclaratoria: Las tres proyecciones a representar se deben corresponder con las        caras visibles de la pieza.
4.- El punto O (proyección vertical O1 y horizontal O2) pertenece al plano proyectante        horizontal dado por sus trazas ( va , ha) y es el centro de la base hexagonal (de 20 mm        de lado) de un prisma recto. La base hexagonal pertenece también al plano proyectante a.        Dibujar las proyecciones horizontal y vertical de la porción de prisma que va desde el        plano proyectante hasta el plano vertical de proyección.
5.- Dadas las proyecciones diédricas (en sistema europeo) de la pieza, realizar la isometría        sin aplicar coeficientes de reducción. Dibuja a escala 1 : 1, tomando las medidas        directamente del dibujo dado y utilizando el sistema de ejes indicado.
6.- Obtener la perspectiva cónica del cuerpo representado por sus proyecciones diédricas        (alzado y planta superior).        Se aplicarán a la perspectiva las dimensiones del cuerpo a escala 1 : 1. El punto de vista V        se encuenta a 60 mm del cuadro y a 50 mm del plano objetivo, en el cual se apoya el        modelo (escala 1 : 1).

Ejercicios Selectividad Julio 2016
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Construir un trapecio conocidas sus bases (B1 = 60 mm, B2 = 40 mm) y sabiendo        que sus otros dos lados miden 30 mm y 50 mm.		Con los datos propuestos no tiene Solución
2.- Determina la verdadera magnitud de la diagonal del cubo de la figura, definido        por sus proyecciones diédricas, mediante la aplicación de un cambio de plano vertical.
3.- Dibujar a mano alzada las proyecciones ortogonales (planta, alzado y perfil izquierdo)        de la pieza indicada, sin tomar medidas, pero manteniendo lo más posible las proporciones.
4.- Determinar la verdadera magnitud de la sección producida por un plano proyectante a        sobre una pirámide recta de base cuadrada.
5.- Dibujar la proyección diédrica que falta en la figura.        - Dibujar en perspectiva isométrica y a escala 1 : 1, la pieza representada por sus          proyecciones diédricas.          Nota: No aplicar coeficientes de reducción y redondear las cotas necesarias a          unidades de mm.
6.- Representar, a escala 2 : 1 el cuerpo dado por sus proyecciones diédricas. Sabiendo        que está apoyado en el plano geometral, en la posición indicada por el abatimiento        de su planta sobre el plano del cuadro.        Notas aclaratorias: (V) es el abatimiento sobre el plano del cuadro del punto de        vista V. La figura está más alejada que el plano del cuadro.
1.- Sabiendo que el foco de una parábola dista de su directriz 20 mm, se pide:        - Determinar la tangente a la parábola que forma 60º con el eje de dicha parábola.        - Determinar el punto de tangencia.
2.- Determinar la verdadera magnitud de la distancia entre los puntos A y B pertenecientes        a la recta r, mediante la aplicación de un cambio de plano vertical.
3.- Dibujar a mano alzada las proyecciones ortogonales (planta, alzado y perfil izquierdo) de        la pieza indicada, sin tomar medidas, pero manteniendo lo más posible las proporciones.
4.- Conocidas las proyecciones diédricas de un cono recto de revolución y dos trazas de un        plano a, se pide:        - Determinar las proyecciones vertical y horizontal de la intersección del plano con el cono.        - Determinar la verdadera magnitud de la intersección.
5.- Acotar la figura plana.
6.- Dibujar la proyección diédrica que falta en la figura.        Dibujar en perspectiva isométrica y a escala 1 : 1, la pieza representada por sus        proyecciones diédricas.        Nota: No aplicar coeficientes de reducción y redondear las cotas necesarias a unidades de mm.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) JuNio 2017
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- La figura representa el contorno de una palanca. Dibujarla a escala 1/2.        Nota aclaratoria: Dejar indicadas las construcciones auxliares e indicar los puntos de tangencia.		Con los datos propuestos no puede completarse la figura.
2.- Construir el triángulo del que se conoce la longitud de su lado AC = 55mm y la longitud        de las medianas mc = 40mm y ma = 55mm.
3.- Dado el triángulo ABC, obtener r2 y sus trazas, sabiendo que la recta r pertenece al plano ABC.
4.- Dadas las vistas de una pieza. Croquizar (a mano alzada, guardando las proporciones        y sin líneas ocultas) su perspectiva isométrica.
5.- La figura representa, la planta y el perfil izquierdo de una pieza. Se pide:               - Dibujar a escala el alzado, incluidas sus líneas ocultas.               - Acotar, a mano alzada, las vistas, considerando que están a escala 1 : 1, en milímetros                 y sin decimales.
1.- Enlazar las rectas r y s mediante 2 arcos de circunferencia de igual radio, siendo los puntos de        enlace T1 y T2.
2.- Dibujar un triángulo, conocidos dos lados y una altura: b = 60 mm, a = 40 mm y ha = 30 mm.
3.- Dibujar las trazas del plano que contiene al punto P y es perpendicular a la recta r.
4.- Dadas las vistas de una pieza se pide:               1. Croquizar (a mano alzada y guardando las proporciones) su perspectiva isométrica.                     Incluir líneas ocultas.               2. Obtener, en el sistema diédrico, la verdadera magnitud de la cara de la pieza que es                     perpendicular al Plano de proyección vertical (XZ) y oblícua a la Línea de Tierra (X).
5.- La figura representa, la planta y el alzado de una pieza. Se pide:               1.- Completar las líneas ocultas que faltan en las vistas (los agujeros son pasantes).               2.- Acotar las vistas, considerando que están a escala 1 : 2, en milímetros sin decimales.               3.- Calcular el volumen en dm3.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) JuLio 2017
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Localizar un punto P interior al triángulo ABC, que equidiste de los lados AB y BC, de forma que el        ángulo APB sea de 120º.        Nota aclaratoria: Resolverlo aplicando el concepto de Arco Capaz.
2.- Dados los ejes de una elipse y un punto exterior P, dibujar una tangente a dicha elipse desde P.        Nota aclaratoria: No es necesario dibujar la elipse.
3.- Dada la traza vertical de un plano P y las proyecciones del punto A, se pide:            1.- Representar la traza horizontal del plano P sabiendo que es perpendicular al primer bisector.            2.- Dibujar las proyecciones de la circunferencia situada en el plano P, que contiene al punto A                 y es tangente a los planos de proyección, determinando los ejes de las cónicas resultantes                 (proyecciones horizontal y vertical).
4.- Dibujar, a escala 1 : 1, la perspectiva isométrica de la pieza dada por sus vistas en el Sistema Europeo.        Notas aclaratorias: No aplicar coeficientes de reducción. Excluir líneas ocultas.
5.-            1.- Croquizar (a mano alzada) la planta superior (vista) y el alzado (con semicorte por el plano                 de simetría), de la forma corpórea dada a escala 1 : 1.            2.- Acotar la pieza para que quede correctamente definida.            Notas aclaratorias: Todos los agujeros son pasantes. Indicar las cotas en milímetros y sin decimales.
1.- Construir un triángulo del que se conocen un lado (l = 80mm), la altura sobre dicho lado (h = 50mm)        y el ángulo opuesto 60º.        Indicar el circuncentro (C), el incentro (I), ortocentro (O) y el baricentro (B).
2.-            1.- Dibujar la hipérbola, conocidos sus vértices (A y B) y uno de sus focos (F´).            2.- Calcular al menos 6 puntos (incluidos los vértices).
3.- Determinar el punto I de intersección de la recta r y el triángulo definido por los puntos A, B y C.
4.- Croquizar (a mano alzada) la perspectiva isométrica de la pieza dada por sus vistas en el Sistema        Europeo.        Nota aclaratoria: Excluir líneas ocultas.
5.-        1.- Croquizar (a mano alzada), en el Sistema Diédrico Europeo, el alzado (A) cortado por el plano              de simetría, la planta superior y el perfil izquierdo.        2.- Acotar las proyecciones diédricas, transponiendo las cotas dadas en perspectiva.        Nota aclaratoria: El agujero es pasante.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) JuNio 2018
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Construir un pentágono regular, conocido uno de los lados (A, B).
2.- Dibujar la pieza dada, a escala 1 : 2, indicando los centros y puntos de tangencia de los        arcos de enlaces utilizados.        Notas aclaratorias: Dibujar solo media pieza. Dejar indicadas las construcciones        auxiliares.
3.- Hallar las proyecciones de una circunferencia situada en el plano a. Sabiendo que es        tangente a los planos de proyección y que pasa por el punto A.        Nota aclaratoria: No es obligatorio dibujar la elipse, pero si sus ejes.
4.- Dibujar las proyecciones, vertical y horizontal, del tetraedro regular que tiene una        de sus caras en el plano vertical de proyección y se encuentra integramente en el        primer cuadrante, sabiendo que una de las aristas de esta cara es el segmento r, dado        por su proyeción vertical r2.
5.- La figura representa la perspectiva isométrica de una pieza. Se pide:               1.- Croquizar la vista de planta superior y la vista de alzado con semicorte, en el               Sistema Europeo.               2.- Acotar la pieza en las proyecciones diédricas transponiendo las medidas de la               perspectiva.
1.- Trazar, en el interior del segmento circular de la figura, una circunferencia que sea        tangente a la cuerda y a la circnferencia dada en el punto T..
2.- Trazar, a escala 1 : 1, la tangente a una parábola cuyo foco dista del eje principal        15 mm, en uno de los puntos de la parábola que distan del eje principal 30mm.
3.- Dibujar en verdadera magnitud el triángulo ABC dado por sus proyecciones.
4.- Croquizar (a mano alzada) la perspectiva caballera de la pieza dada por sus         proyecciones diédricas (Sist. Europeo).         Nota: No dibujar las líneas ocultas, posicionar la pieza de tal forma que el perfil         izquierdo se vea en verdadera magnitud.
5.-           A) La figura representa una chapa de espesor 10 mm. Croquizar, en la vista dada, la                sección abatida.           B) ¿Es correcta la línea señalada? (Si/No):__________           C) ¿Qué cotas sobran en la pieza? (tacharlas en la figura)                ¿Por qué sobran? : ______________________________           D) Croquizar el alzado en vista y la planta superior con los cortes necesarios para                definir el objeto sin necesidad de dibujar líneas ocultas.                Acotar sin consignar sus valores numéricos.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) Julio 2018
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Construir un trapecio conocidas sus bases (B1 = 60mm, B2 = 30mm) y sabiendo que        sus otros lados miden 40mm y 50mm.
2.- Se desea construir un puente cuya estructura tiene un vano (ojo) parabólico cuyos        datos en, dm, se indican en la figura.        Obtener, a escala 1:100, la distancia 1 (intersección de la parábola con el puente) y        la distancia 2 (intersección de la parábola con el suelo).
3.- Determinar la distancia entre dos rectas paralelas, definidas por sus proyecciones        diédricas horizontales (r1 y s1) y verticales (r2 y s2).
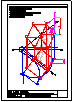
4.- A) Dibujar una pirámide recta de base hexagonal regular apoyada en el primer              cuadrante del plano horizontal de proyección, sabiendo que una de las aristas de              dicha base es el segmento r, y que su altura es 3r.        B) Dibujar la sección producida, en la pirámide, por el plano a (proyecciones              y verdadera magnitud).
5.- A) Acotar la pieza dada para su correcta definición dimensional. Realizar en el               perfil un corte parcial, para poder acotar correctamente los agujeros.        B) Croquizar la perspectiva axonométrica de la pieza, sin indicar las líneas ocultas.        Notas aclaratorias: La pieza está representada a escala 1:2. Acotar en mm, sin decimales.
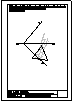
1.- Dibujar, a escala 1 : 1, la figura obteniendo las correspondientes curvas de enlaces,        señalando los centros y puntos de tangencia.        NOTA: Dibujar solo la parte exterior (desde A hasta B).
2.- Conocidos los diámetros conjugados de una elipse, dibujar su contorno.
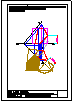
3.- Una pelota desliza por un tejado desde el punto A. Determinar las proyecciones (r1, r2) de la        trayectoria seguida por la pelota sobre el tejado y el punto (P1, P2) en el suelo, suponiendo        que define una trayectoria recta.
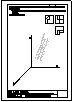
4.- Conocidas dos vistas de una pieza (alzado y planta supertior), en el Sistema Europeo, se pide:            1. Dibujar la vista lateral derecha, incluyendo líneas ocultas.            2. Croquizar, respetando las proporciones, la perspectiva caballera de la pieza.
5.-      A) Indicar qué cotas están mal representadas: _____________________________            ____________________________________________________________      B) Qué superficie geométrica representan las cotas            Ø25 y 2x45º __________________________________________________            ____________________________________________________________      C) Cómo se llama el corte representado en el alzado:            ____________________________________________________________      D) La pieza 1, representada en perspectiva isométrica, tiene ensu interior un hueco en el            que se acopla, sin holguras, la pieza 2.            Croquizar y acotar el alzado de la pieza 1 con un corte a 90º.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) Junio 2019
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Hallar las circunferencias tangentes a la dada por el punto de tangencia A, y que a la        vez sean tangentes a la recta r.
2.- Una elipse viene definida por el eje mayor AB y por el punto P. Dibujar la tangente y        la normal a la elipse en dicho punto P.
3.- Dado el plano P y la recta r contenida en él, dibujar otra recta que pertenezca al plano        y forme 30º con la dada.
4.-Se representa la proyección horizontal de un tetraedro apoyado en el Plano Horizontal.        Se pide:        A) Construir el tetraedro regular, en planta y en alzado ( 1 punto ).        B) La sección, en proyecciones horizontal y vertical y en verdadera magnitud, que        produce en el tetraedro el plano a ( 1 punto ).        C) La sección, en proyecciones horizontal y vertical, que produce en el tetraedro        el plano b ( 0,5 puntos ).
5.- A mano alzada, croquizar las vistas diédricas necesarias de la pieza dada en        isométrico, de acuerdo con el sistema europeo de proyecciones, aplicando cortes        y/o secciones si fuera preciso y disponiendo las cotas para completar su definición.
1.- La circunferencia dibujada representa un depósito de vino cilíndrico visto en planta.        Los puntos A y B representan dos columnas.        Dibujar el depósito de vino cilíndrico con mayor diámetro que cabe entre las dos        columnas y el depósito dado.        (Utilizar los conceptos de potencia , eje radical y centro radical).
2.- Trazar la tangente y la normal a la hipérbola de la figura, en el punto P.        Dibujar también las asíntotas.
3.- Hallar el ángulo en verdadera magnitud que forman los planos representados.
4.- Dadas las vistas diédricas de una pieza a Escala 1 : 2, dibujar la perspectiva        isométrica, siguiendo la disposición de ejes mostrada, a Escala 3 : 4 tomando        medidas directamente del dibujo dado y sin aplicar coeficiente de reducción.
5.- A mano alzada, croquizar las vistas diédricas necesarias de la pieza dada en        isométrico, de acuerdo con el sistema europeo de de proyección, aplicando cortes        si fuera preciso y disponiendo las cotas para completar su definición.        Todos los agujeros son pasantes y la pieza tiene dos planos de simetría perpendiculares.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) Julio 2019
	OPCIÓN A		OPCIÓN B
	DATOS	SOLUCIÓN	DATOS	SOLUCIÓN
1.- Dibujar todas las circunferencias que son tangentes a la recta dada y pasan por         los puntos A y B. Definir claramente los puntos de tangencia. (Usar conceptos         de potencia y eje radical).
2.- Dados algunos elementos básicos de una parábola (directriz, eje, vértice) y un        punto P de la misma, dibujar la tangente y la normal a la parábola por dicho        punto P.
3.- Hallar la intersección de tres planos ( a , b ,c ), conocidas sus trazas vertical y horizontal.
4.-Determinar la sección producida por el plano representado, que es paralelo a la línea de        tierra, sobre el prisma dado por sus proyecciones horizontal y vertical. Hallar también        su verdadera magnitud.
5.- A mano alzada, croquizar las vistas necesarias de la pieza dada en isométrico, de        acuerdo con el sistema europeo de proyección, aplicando cortes si fuera preciso y        disponiendo las cotas para completar su definición.
1.- Dibujar la circunferencia que es tangente a la dada por el punto A y a la vez pasa        por el punto exterior B.
2.- Dibujar las tangentes por los puntos A y B de la parábola cuyo foco es el punto F.
3.- Dibujar las trazas del plano que contiene a la recta r y es paralela a la recta s.
4.- La perspectiva de la figura representa una pieza con base inferior un        hexágono regular. La pieza tiene un hueco interior, cuya base es        rectangular y su centro coincide con el centro del hexágono.        Dibujar a escala 3 : 4 las proyecciones diédricas de planta, alzado y        perfil derecho, según el Sistema Europeo.        NOTA: Posicionar las vistas de tal forma que la base superior sea        proyectante sobre el plano de perfil.
5.- A mano alzada, croquizar las vistas diédricas necesarias de la pieza dada        en isométrico, de acuerdo con el sistema europeo de proyección, aplicando        cortes si fuera preciso y disponiendo las cotas para completar su definición.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) Julio 2020
	OPCIÓN ÚNICA
	DATOS		SOLUCIÓN
1.- Dada la circunferencia de centro el punto O y los puntos A y B, dibujar las circunferencias         tangentes a la dada y que pasen por dichos puntos.         Si el dibujo está realizado a Escala 1 : 500, determinar la longitud real de los diámetros         de dichas circunferencias tangentes.
2.- Dado el semieje mayor y el semieje menor de una elipse:         • dibujar la elipse con al menos 12 puntos.         • hallar las tangentes de dicha elipse que pasan por el punto P exterior.         • hallar la tangente y la normal a la elipse por el punto Q que pertenece a ella.
3.- Definida una parábola por su eje de simetría, su recta directriz y su foco, queremos        determinar los puntos de intersección de la recta "r" con dicha parábola.
4.-Dado el plano a y un punto P que pertenece al mismo, dibujar un hexágono regular       de lado 35mm, que esté contenido en dicho plano, que tenga como centro el punto P        y que tenga dos lados horizontales.        Representar dicho hexágono en verdadera magnitud, en planta y en alzado.
5.- El segmento AB es el lado de un triángulo equilátero contenido en un plano        que forma 45º con el plano horizontal de proyección.        Dibujar el triángulo en verdadera magnitud y en las proyecciones en planta        y alzado, (representar una sola de las soluciones posibles).
6.- Un cubo tiene una cara en el plano dado, está encima de dicho plano y tiene una        arista en la traza horizontal del plano, siendo A y B los extremos de dicha arista.        Dibujar el cubo en ambas proyecciones diédricas horizontal y vertical.
7.- Hallar la sección producida por el plano P en el prisma recto de base cuadrangular        y también, su verdadera magnitud.        Errata en el enunciado, dice ... prisma recto .... , debe decir .... pirámide recta .....
8.- Dadas las vistas diédricas de una pieza a Escala 1 : 5, dibujar la perspectiva isométrica        siguiendo la disposición de ejes mostrada y a Escala 1 : 2.        (no es necesario aplicar coeficientes de reducción).
9.- Dibujar las vistas diédricas necesarias de la figura dada. Se pueden tomar medidas        directamente de la vista isométrica o utilizar otras que mantengan la proporcionalidad.        Todos los agujeros son pasantes.        Aplicar cortes, si fuera necesario.        Disponer sobre dichas vistas las cotas que creas necesarias (NO ES NECESARIO        INCORPORAR LAS CIFRAS).
10.- Dibujar las vistas diédricas necesarias de la figura dada, aplicar cortes y acotar.          Utilizar una Escala adecuada para el espacio disponible.          Todos los agujeros son pasantes.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) Septiembre 2020
	OPCIÓN ÚNICA
1.- Dada la recta "r" y los puntos A y B, dibujar las circunferencias tangentes a la        recta dada y que pasen por los puntos A y B dados.        Si el dibujo está realizado a Escala 1 : 750, determinar la longitud real de los        diámetros de dichas circunferencias tangentes.
2.- Construir una hipérbola dados los focos F y F´ y los vértices A y B (al menos        5 puntos en cada rama)        Desde el punto P exterior, determinar las tangentes a dicha hipérbola.
3.- Trazar un cuadrado inscrito en la elipse dada por sus ejes.
4.- Hallar el ángulo en verdadera magnitud que forman las dos rectas dadas.
5.- Dibujar dos planos paralelos al dado que estén a 30 mm del representado.
6.- Dadas las vistas diédricas de una pieza dibujadas a Escala 1 : 2, representarla        en perspectiva caballera a Escala 1 : 1        (no es necesario aplicar coeficientes de reducción)
7.- Hallar la sección producida por el plano a en la pirámide        recta de base pentagonal y también, su verdadera magnitud.
8.- Hallar el punto de entrada y de salida de la recta "r" en la esfera dada por sus        proyecciones horizontal y vertical. Mostrar las partes ocultas y las partes vistas        en cada una de las proyecciones.        Determinar la verdadera magnitud del trozo de recta que queda dentro de la esfera.
9.- Dibujar las vistas diédricas necesarias de la figura dada. Se pueden tomar medidas        directamente de la vista isométrica o utilizar otras que mantengan la proporcionalidad.        Todos los agujeros son pasantes.        Aplicar cortes, si fuera necesario.        Disponer sobre dichas vistas las cotas que creas necesarias        (NO ES NECESARIO INCORPORAR LAS CIFRAS)
10.- Dibujar las vistas diédricas necesarias de la figura dada, aplicar cortes y acotar.          Utilizar una Escala adecuada para el espacio disponible.          Todos los agujeros son pasantes.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) junio 2021
	OPCIÓN ÚNICA
1.- Reproducir la figura dada a escala 1 : 1, marcando claramente los centros de los        arcos y los puntos de tangencia.
2.- Construir la parábola dados su eje, su directriz y su foco (determinar al menos 7 puntos)        Desde el punto exterior P dibujar las tangentes a dicha parábola.
3.- Dados el eje mayor y los focos de una elipse, determinar las tangentes a dicha elipse        desde un punto exterior P.
4.- Dado el plano a, dibujar en él un cuadrado de lado 30mm y dibujar también las proyecciones        horizontal y vertical de dicho cuadrado.
5.- Dada la recta r y un punto A, dibujar otra recta perpendicular a la dada que pase por        el punto y por la recta r.
6.- Dibujar un tetraedro regular apoyado en el plano horizontal sobre el vértice A, siendo        la cara opuesta paralela a dicho plano horizontal. Se sabe que una arista de esa cara        horizontal forma 45º con el plano vertical de proyección. Las aristas del tetraedro son        de 50 mm.        Representar el tetraedro en sus proyecciones horizontal y vertical, definiendo aristas        vistas y ocultas.
7.- Dadas las vistas diédricas de una pieza, dibujar a Escala 1 : 1 la perspectiva isométrica        siguiendo la disposición de ejes mostrada.        (sin aplicar coeficientes de reducción).        Incluir sólo aristas vistas.
8.- Hallar la sección producida sobre el cono dado, por un plano proyectante vertical a.        Definirla en planta y en alzado con al menos 8 puntos.
9.- Dibujar las vistas diédricas necesarias de la figura dada (con instrumentod de dibujo ó a        mano alzada). Se pueden tomar medidas directamente de la vista isométrica o utilizar        otras que mantengan la proporcionalidad. Todos los agujeros son pasantes.        Aplicar cortes, si fuera necesario.        Disponer sobre dichas vistas las cotas que creas necesarias        (NO ES NECESARIO INCORPORAR LAS CIFRAS)
10.- A mano alzada y manteniendo las proporciones, croquizar las vistas diédricas          necesarias de la pieza dada, aplicar cortes y acotar         (solo líneas de cota). Todos los agujeros son pasantes.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) JULIO 2021
	OPCIÓN ÚNICA
1.- Reproducir la figura dada a escala 2:3, marcando claramente los centros de los arcos y los        puntos de tangencia.
2.- Desde un punto P, se desea trazar las rectas tangentes a una elipse de ejes AB = 70mm y        CD = 53 mm.        El punto P se halla sobre la prolongación de AB y a 25 mm de B.
3.- Trazar la hipérbola conocidos los vértices A y B en el eje real y las asíntotas.        Dibujar al menos 4 puntos en cada rama.
4.- Dado el plano a y un punto P exterior, determinar la distancia en verdadera magnitud        del punto al plano.
5.- Hallar el ángulo en verdadera magnitud que forman las dos rectas dadas.
6.- Hallar la intersección de la recta dada con el tronco de cono representado y la verdadera         magnitud del trozo de recta que queda dentro del tronco de cono.
7.- Hallar el ángulo en verdadera magnitud que forman las dos rectas dadas.
8.- Nos dan las proyecciones diédricas de una pieza y nos piden que dibujemos la         perspectiva isométrica conforme al sistema de coordenadas dado. Dibujarla         a escala 1 : 1 y sin aplicar coeficientes de reducción. Aristas vistas y ocultas.
9.- Dibujar las vistas diédricas necesarias de la figura dada (con instrumentos de         dibujo ó a mano alzada). Se pueden tomar medidas directamente de la vista         isométrica o utilizar otras que mantengan la proporcionalidad. Todos los agujeros         son pasantes. Aplicar cortes, si fuera necesario.
10.- Croquizar a mano alzada las vistas necesarias de la figura dada, aplicar cortes           y acotar. Todos los agujeros son pasantes.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) junio 2022
	OPCIÓN ÚNICA
1.- Dadas dos circunferencias con centros C1 y C2 y un punto P en una de las circunferencias, hallar las        circunferencias tangentes a ambas y que pasan por el punto P.
2.- Dibujar una hipérbola equilátera (eje real = eje imaginario), conocidos sus 2 focos, representando        al menos 10 puntos de sus dos ramas (5 puntos por cada rama).        Desdeun punto exterior a dicha hipérbola, situado a 40 mm de F y a 75 mm de F´, trazar las        tangentes a la hipérbola.
3.- En una excavación arqueológica se ha encontrado un objeto extraño. Tiene una sección formada por        dos curvas, una de forma semielíptica y otra parabólica. Dibujar a escala 2 : 1 ese objeto tan extraño        con suficientes puntos intermedios.
4.- En una excavación arqueológica se ha encontrado un objeto extraño. Tiene una sección formada por        dos curvas, una de forma semielíptica y otra parabólica. Dibujar a escala 2 : 1 ese objeto tan extraño        con suficientes puntos intermedios.
5.- Dados el punto A, la recta R y el plano P, se pide:        1. Dibujar las proyecciones horizontal y vertical de una recta S paralela a la R y que pase por el punto A.        2. Hallar las trazas de un plano Q que contenga a la recta S sea perpendicular al plano P.        3. Hallar la intersección de los planos P y Q.        4. Hallar la verdadera magnitud de la semirecta de P y Q que queda dentro del primer diedro.
6.- El punto O pertenece al plano P representado por sus trazas horizontal y vertical. Queremos dibujar        una pirámide recta de base hexagonal regular de centro O y de altura 50 mm. Dicha base hexagonal        se apoya en el plano P, tiene dos lados opuesto horizontales y la arista mide 30 mm.        Dibujar las proyecciones horizontal y vertical de la pirámide descrita.
7.- Se conocen las proyecciones horizontal y vertical de un punto A y de una recta R. Se pide:        1. Determinar las trazas del plano P que contiene al punto A y a la recta R.        2. Hallar las proyecciones horizontal y vertical de la recta S que pasa por el punto A y forma 60º             con la recta R. (Si hubiera dos soluciones, dar las dos).
8.- Dadas las proyecciones diédricas en el primer diedro (Sistema Europeo) a escala 1 : 2, se pide:        * Dibujar la perspectiva caballera a escala 1 : 1, sin aplicar coeficientes de reducción, tomando           medidas directamente del dibujo dado. Representar las aristas vistas y las ocultas.
9.- Dibujar las vistas diédricas necesarias de la figura dada (con instrumentos de dibujo ó a mano alzada).        Se pueden tomar medidas directamente de la vista isométrica o utilizar otras que mantengan la        proporcionalidad. Todos los agujeros son pasantes.        Aplicar cortes, si fuera necesario.        Disponer sobre dichas vistas las cotas que creas necesarias        (NO ES NECESARIO INCORPORAR LAS CIFRAS).
10.- Se muestra una figura en isométrico a escala 1 : 2. Se incluye una vista en planta de dicha           figura, dibujada también a escala 1 : 2 (Sistema Europeo)           Se pide:            * Plantear en la vista en planta la traza de un corte total a lo largo del eje de simetría.            * Dibujar sobre la vista en planta, la vista de alzado, ejecutando en ella el corte propuesto.               (Estimar las alturas midiendo directamente en la figura dada).            * Dibujar la vista lateral si fuera necesaria.            * Disponer en las vistas las cotas correspondientes.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) julio 2022
	OPCIÓN ÚNICA
1.- Reproducir la figura a escala 3:2, marcando claramente los centros de los arcos y los puntos de tangencia.         (No borrar construcciones auxiliares).
2.- De una parábola se conocen el Foco, una tangente t y su punto de tangencia T.         º    Hallar el eje y el vértice de la parábola.         º    Trazar la recta tangente a la cónica paralela a la recta dada r y determinar su punto de tangencia.
3.- Definida una elipse por su eje mayor y sus focos, dibujar por el punto P exterior las dos        tangentes a dicha elipse. No es necesario dibujar la elipse.        Describir textualmente los pasos que es necesario dar para alcanzar la solución pedida.
4.- Hallar la distancia de un punto P al plano a (representarla en las proyecciones horizontal y        vertical y hallar su verdadera magnitud).
5.- El polígono ABCD está contenido en el plano a . Dibujar su proyección en planta y hallar        la verdadera magnitud.
6.- Dibujar un tetraedro regular cuya arista tenga 50 mm, tenga una cara apoyada en el plano        horizontal y una de las aristas de su base es la línea A1 B1. Y obtener los puntos de intersección        de la recta r con las caras del tetraedro.
7.- Se tiene la proyección horizontal de un prisma recto de base rectangular apoyado en el plano        horizontal de proyección. La altura del prisma son 40 mm. Representar la proyección vertical        del prisma y la sección producida por el plano a , tanto en proyección horizontal como en la vertical.
8.- Dadas las vistas diédricas de una pieza a escala 1:1, dibujar con instrumentos de dibujo a escala 2:1        la perspectiva isométrica siguiendo la disposición de ejes mostrada. Tomar medidas directamente        de las vistas dadas.        Dibujar aristas vistas y ocultas.        (no es necesario aplicar coeficientes de reducción).
9.- Dibujar las vistas diédricas necesarias de la figura dada (con instrumentos de dibujo ó a mano alzada).        Se pueden tomar medidas directamente de la vista isométrica o utilizar otras que mantengan la        proporcionalidad. Todos los agujeros son pasantes.        Aplicar cortes, si fuera necesario.        Disponer sobre dichas vistas las cotas que creas necesarias (NO ES NECESARIO INCORPORAR LAS CIFRAS)
10.- A mano alzada y manteniendo las proporciones, croquizar las vistas diédricas necesarias de la          pieza dada, aplicar cortes y acotar (sólo líneas de cota). Todos los agujeros son pasantes.

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) junio 2023
	OPCIÓN ÚNICA
1.- Una vista frontal de una arandela se compone de dos circunferencias concéntricas, una interior        y otra exterior.        Dibujar la arandela, con las siguientes condiciones:        - La circunferencia exterior es tangente a la recta t..        - La circunferencia interior tiene 20mm menos de radio que la exterior y pasa por los puntos A y B.        - Dibujar las dos soluciones posibles.
2.- Hallar, sin dibujar la parábola, los puntos de intersección de la recta r con la parábola definida por        su directriz (d) y su foco (F).
3.- Un túnel-invernadero para el cultivo de hortalizas tiene una sección transversal de forma        semielíptica, siendo su anchura total en el suelo de 3 metros. Se sabe que la altura máxima        dentro del túnel es de 2,5 metros.        Dibujar una sección transversal semielíptica de dicho túnel, con al menos 9 puntos y posicionar        claramente uno de los focos.        Dibujar dicha sección semielíptica a una escala adecuada, aprovechando el espacio disponible        e indicar dicha escala en el dibujo.
4.- Dadas las proyecciones horizontal y vertical de larecta r y del punto P.        - Trazar por el punto P el plano a perpendicular a la recta r. (1 punto)        - Hallar el punto de intersección entre la recta r y el plano a hallado. (1 punto)
5.- Dado el triángulo ABC, representado por sus proyecciones horizontal y vertical, y la recta r.        Se pide:        - Hallar la intersección de la recta r con el plano triangular ABC (0,5 puntos)        - Hallar en dicho triángulo un hexágono regular de lado 18 mm, cuyo centro sea el punto de          intersección hallado anteriormente.        Y trasladar los vértices del hexágono a las proyecciones horizontal y vertical. (1,5 puntos)
6.- Representar las proyecciones horizontal y vertical de un cubo de 50 mm de arista, apoyado        en una de sus caras en el plano a dado por sus trazas. Tener en cuenta lo siguiente:        • El punto C es un vértice del cubo.        • Una arista que pasa por C y se apoya en el plano a, es horizontal.        • El cubo está integramente en el primer cuadrante.
7.- Hallar la verdadera magnitud de la sección oblicua generada por el plano a sobre el prisma        recto de base triangular apoyado en el suelo y de 45 mm de altura, representado sólo por su        proyección horizontal.
8.- Dadas las vistas de planta, alzado y lateral derecho de una pieza, en sistema europeo        (primer diedro), y representada a escala 1 : 3, se pide:           - Dibujar la perspectiva caballera a escala 1 : 1, tomando las medidas directamente           del dibujo y sin aplicar coeficientes de reducción.
9.- A mano alzada y manteniendo las proporciones, croquizar las vistas diédricas necesarias de        la pieza dada, aplicar cortes y acotar (sólo líneas de cota). Todos los agujeros y hendiduras        son pasantes.
10.- Dada una pieza por su representación isométrica (sin coeficientes de reducción), dibujar las           vistas diédricas de planta, alzado y vista lateral izquierda (según el sistema europeo           de proyección), tomando medidas directamente de la figura. Realizar la acotación completa            siguiendo las normas UNE.

Descargar el fichero de datos, JULIO 2023, desde esta página

Ejercicios DE EVALUACIÓN DE BACHILLERATO PARA ACCESO A LA UNIVERSIDAD (EBAU) julio 2023
	OPCIÓN ÚNICA
1.- Reproducir la figura dada a escala 1:1, marcando claramente los centros de los arcos y los        puntos de tangencia.
2.- Dado un punto P de la Elipse, una tangente t y el eje menor CD, dibujar el punto de tangencia        de la elipse con t.
3.- Dados el foco F y los puntos A y B de una parábola, se pide:        - Dibujar la directriz, el eje y el vértice de la parábola. (de las dos directrices posibles, tomar          la inferior).        - Dibujar la parábola, obteniendo dos puntos más a cada lado del eje.        - Traza la tangente a la cónica en los puntos A y B.
4.- Determinar el ángulo en verdadera magnitud que forman el plano a y la recta r.
5.- De un plano a se conocen su traza horizontal a1 y su traza vertical abatida a0. También       se conoce el abatimiento del polígono ABCD contenido en dicho plano a. Se pide:  1. Dibujar la traza vertical del plano a2.  2. Dibujar las proyecciones horizontal y vertical del polígono ABCD.
6.- Hallar la distancia en verdadera magnitud desde un punto A dado por sus proyecciones       horizontal y vertical, hasta el plano a paralelo a la línea de tierra y dado por sus trazas       horizontal y vertical.       Dibujar también, en proyección horizontal y vertical, una línea cualquiera paralela al plano a,       que no sea horizontal y que pase por el punto A.
7.- Dada la proyección horizontal de la base pentagonal regular de una pirámide recta y las       proyecciones horizontal y vertical de su vértice V. Hallar:       1. La representación completa en planta y alzado de la pirámide recta de base pentagonal.       2. Los puntos de intersección de la recta r con dicha pirámide.       3. Ángulo en verdadera magnitud que forman las caras laterales de la pirámide con el            plano horizontal.
8.- Dadas las vistas diédricas de una pieza, dibujar con instrumentos de dibujo a escala 3:2       la perspectiva isométrica siguiendo la disposición de ejes mostrada. Tomar medidas       directamente de las vistas dadas. Dibujar aristas vistas y ocultas.       (no es necesario aplicar coeficientes de reducción).
9.- Dada una pieza por su representación isométrica (sin coeficientes de reducción aplicados),       dibujar las vistas diédricas de planta, alzado y vista lateral izquierda (según el sistema       europeo de proyección), tomando medidas directamente de la figura.       Realizar la acotación completa siguiendo las normas UNE.
10.- Se muestra una figura afectada por un plano de corte total, ejecutado a lo largo del eje          de simetría. Se incluye además una vista en planta de dicha figura, a escala 1:1, con la          traza de corte A-A propuesta. Se pide:          • Dibujar sobre la vista en planta, la vista de alzado, ejecutando en ella el corte propuesto A-A.          (Estimar las alturas midiendo directamente de la figura dada).          • Disponer las cotas necesarias en dicho alzado.