|
Ejercicios Selectividad Junio 2015 (Ordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
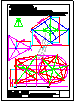
1.- Primer Bloque
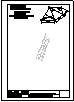
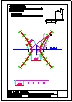
Dibuja a escala 1 : 500 la figura con los datos
siguientes:
1) TRIÁNGULO ABC: AC = 50 m (HORIZONTAL).
MEDIANA SOBRE AC = 30 m.
ALTURA SOBRE AB = 35 m.
2) TRIÁNGULO ACD: ÁNGULO EN A = 30º.
ALTURA SOBRE AC = 35 m.
3) TRIÁNGULO ADE: ÁNGULO EN E = 120º.
EA / DE = 1 / 2
|
|
|
|
|
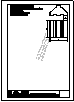
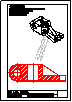
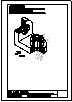
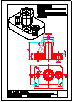
2.- Primer Bloque
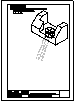
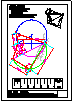
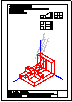
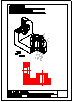
Dada la perspectiva de la ilustración, se pide:
1) Dibujar el alzado en semicorte. Toma las
medidas directamente de la imagen.
2) Acota.
|
|
|
|
|
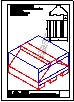
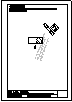
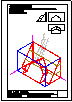
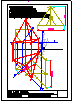
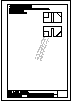
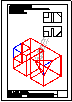
3.- Primer Bloque
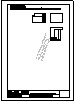
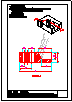
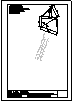
Dadas las vistas diédricas ortográficas de la pieza,
dibuja su perspectiva axonométrica isométrica.
Dimensionar a voluntad, guardando las
proporciones de las vistas.
|
|
|
|
|
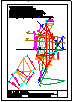
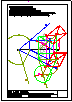
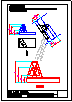
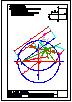
1.- Segundo bloque
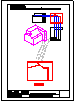
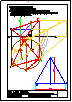
Dibujar las proyecciones de un triángulo ABC
con los datos siguientes:
1) Un vértice es el punto A(-50,30,40)
2) El vértice B tiene de coordenadas (20,50,70)
3) La altura sobre el lado AB es paralela al
segundo bisector y pasa por el punto medio del
lado AB.
4) El vértice C está en el plano vertical.
|
|
|
|
|
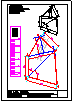
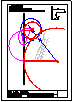
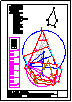
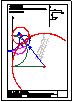
1.- Primer Bloque
Dibuja las circunferencias tangentes a R y S y
pasen por el punto P.
|
|
|
|
|
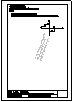
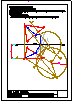
2.- Primer Bloque
Dadas las vistas diédricas ortográficas de la
pieza, dibuja su perspectiva caballera.
Dimensionar a voluntad, guardando las
proporciones de las vistas. Datos de la perspectiva:
j =135º; C. R. = 1 / 2. |
|
|
|
|
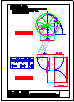
3.- Primer Bloque
Dibuja un ciclo de hipocicloide con los siguientes
datos:
1) Radio de la base = 90 mm.
2) Radio de la ruleta = 30 mm.
|
|
|
|
|
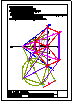
1.- Segundo bloque
Los puntos A(0,60,50) y B(-50,Y,20) definen el
lado de un triángulo equilátero contenido en un
plano que pasa por la L. T. y cuyo vértice C tiene
el mayor alejamiento posible.
Los vértices de este triángulo lo son de un
tetraedro regular.
Dibujar sus proyecciones de modo que el poliedro
esté lo más alto posible respecto al P. H.
|
|
|
|
|
|
Ejercicios Selectividad Julio 2015 (extraordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
Dibuja el triángulo ABC con los datos siguientes:
A-B = 110 mm.
Altura sobre A-B = 80 mm.
Mediana sobre B-C = 80 mm.
Determina el punto del lado B-C que equidista del
vértice C y del lado A-B.
|
|
|
|
|
2.- Primer Bloque
Dada la perspectiva de la ilustración, se pide:
1) Dibujar el alzado en corte total a escala 1 : 1.
Según la dirección señalada.
2) Acota todo lo posible.
|
|
|
|
|
3.- Primer Bloque
Dadas las vistas diédricas ortográficas de la
pieza, dibuja su perspectiva caballera.
Dimensionar a voluntad, guardando las
proporcionesde las vistas.
Datos: j = 135º; C. R. = 3 / 4
|
|
|
|
|
1.- Segundo bloque
Los puntos A (0,20,10) y B (-20,40,50) definen
el lado de un hexágono regular. Dibuja sus
proyecciones sabiendo que el centro tiene
30 mm de cota y el máximo alejamiento posible.
|
|
|
|
|
1.- Primer Bloque
Dada una circunferencia de radio 50 mm, se pide:
- Inscribe un polígono regular de 7 lados.
- Dibuja sus dos polígonos estrellados.
|
|
|
|
|
2.- Primer Bloque
Dadas las vistas diédricas ortográficas de la
pieza, dibuja su perspectiva axonométrica
isométrica.
Dimensiona a voluntad, guardando las
proporciones de las vistas.
|
|
|
|
|
3.- Primer Bloque
Dadas dos circunferencias según croquis, se pide:
- Dibuja el lugar geométrico de
los centros de las circunferencias tangentes
exteriores a ambas.
- Dibuja la solución que sea tangente a la
circunferencia de radio 30 mm en el punto
P señalado.
|
|
|
|
|
1.- Segundo bloque
Los puntos A (-70,50,60) y H (-10,50,60) definen
la diagonal principal de un hexaedro regular.
Dibuja sus proyecciones sabiendo que uno de los
vértices que está unido con el A tiene de cota
40 mm y el menor alejamiento posible.
|
|
|
|
|
|
Ejercicios Selectividad Junio 2016 (Ordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
Realiza el ejercicio de la ilustración a escala natural.
En el trabajo se han de apreciar las operaciones que
realices.
Haz el dibujo en la hoja en posición apaisada.
|
|
|
|
|
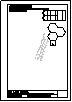
2.- Primer Bloque
Dadas las vistas de la ilustración, halla su perspectiva
caballera según los siguientes datos:
g = 135º; coeficiente de reducción = 1/2.
Realiza la perspectiva a escala 2/1.
|
|
|
|
|
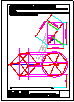
3.- Primer Bloque
Dado el croquis adjunto, construir la figura a escala
adecuada con los siguientes datos:
A) Triángulo BCE:
B-E = 100 m
Altura sobre B-C = 85 m.
Mediana sobre B-E = 85 m.
B) Triángulo ABE:
Altura sobre A-E = 70 m.
Altura sobre A-B = 60 m.
C) Triángulo CDE:
Altura sobre C-E = 50 m.
Altura sobre C-D = 85 m.
|
|
|
|
|
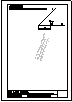
1.- Segundo bloque
Los puntos A(-20, 20, 10) y C(-20, 60, 45) definen la
diagonal de un cuadrado. Dibujar sus proyecciones
sabiendo que tiene otro vértice en el primer plano
bisector, lo más a la izquierda posible.
|
|
|
|
|
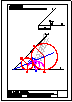
1.- Primer Bloque
Realiza el ejercicio de la ilustración a escala natural.
En el trabajo se han de apreciar las operaciones
auxiliares que realices.
|
|
|
|
|
2.- Primer Bloque
Dadas las vistas de la ilustración. Halla su perspectiva
isométrica sin aplicar coeficiente de reducción.
Deduce las medidas tomando como referencia las que
se adjuntan. Aplica la escala 1 : 2.
|
|
|
|
|
3.- Primer Bloque
Dado el croquis adjunto, construir la figura a escala
adecuada con los siguientes datos:
A-C = 60 m.
A-D = 80 m.
A-E = D-E = B-A
Ángulo ACD = 105º
Ángulo AED = 120º
Ángulo EBC = 75º
|
|
|
|
|
1.- Segundo bloque
La recta r´-r y la paralela a ella que pasa por b´- b
determinan un plano a que contiene una cara de
un hexaedro regular. Dicha cara tiene un vértice
en b´- b y un lado en la recta r´- r. Se pide hallar
las proyecciones del poliedro cuando está en el
primer diedro.
|
|
|
|
|
|
Ejercicios Selectividad Julio 2016 (Extraordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
Realiza el ejercicio de la ilustración a escala natural.
En el trabajo se han de apreciar las operaciones
auxiliares que realices.
|
|
|
|
|
2.- Primer Bloque
Dada la vista en planta, dibuja un alzado acorde
con la planta dada, incluyendo alguna sección si
se considera necesario.
Acota en la medida de lo posible, respetando las
normas. Toma medidas directamente sobre la
planta dada, que está dibujada a escala 1:1.
|
|
|
|
|
3.- Primer Bloque
Dibuja un ciclo de epicicloide con los datos siguientes:
Radio de la base = 40 mm.
Radio de la ruleta = 15 mm.
|
|
|
|
|
1.- Segundo bloque
El plano a(-50, 65, 40) contiene un pentágono regular
cuyo centro es el punto O(0, 25, Z). Dibujar sus
proyecciones sabiendo que tiene un vértice en el plano
vertical. El pentágono está en el primer cuadrante y
es el más pequeño posible.
|
|
|
|
|
1.- Primer Bloque
Realiza el ejercicio de la ilustración a escala natural.
En el trabajo se han de apreciar las operaciones
auxiliares que realices.
|
|
|
|
|
2.- Primer Bloque
Dadas las vistas de la ilustración. Halla su perspectiva
isométrica sin aplicar coeficiente de reducción.
|
|
|
|
|
3.- Primer Bloque
Dibuja, a escala conveniente, la figura dada en croquis.
|
|
|
|
|
1.- Segundo bloque
El plano a está determinado por los puntos P (-50,0,0),
N(0, 50,0) y M (0,0,60). Se pide dibujar las
proyecciones de un hexaedro regular que apoya con
una cara en dicho plano, sabiendo que una arista de
esa cara está en el plano horizontal de proyección.
Los extremos de dicha arista tienen de alejamiento
20 y 50 mm. El poliedro está en el primer cuadrante.
|
|
|
|
|
|
EVALUACIÓN DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2017 (Ordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
Construye la figura de la ilustración a escala 1 : 250.
Datos:
a) AC = 30 metros
b) AD = 40 metros
c) AE = DE = BC
d) Ángulo ACD = 105º
e) Ángulo AED = 120º
f) Ángulo B = 75º
|
|
|
|
|
2.- Primer Bloque
Dibuja un ciclo de la CICLOIDE que describe el punto P
de la circunferencia de centro O1 y radio 20 mm
(RULETA).
|
|
|
|
|
3.- Primer Bloque
Dada la figura en perspectiva axonométrica
isométrica, se pide dibujar a escala 1 :1.
1) El ALZADO.
2) El PERFIL, con el CORTE que consideres más adecuado.
Tomar las medidas directamente de la figura.
No utilizar el coeficiente de reducción.
|
|
|
|
|
1.- Segundo bloque
Dibuja las proyecciones de un triángulo escaleno de
lados AB = 80 mm, BC = 50 mm y AC = 100 mm.
El lado AB está sobre la recta r y el punto B a la
derecha de A, el vértice C tiene 15 mm de
cota y el menor alejamiento posible.
|
|
|
|
|
1.- Primer Bloque
Dado el croquis de la figura se pide:
1.- Dibujar el plano a escala 1 : 1000
2.- Construir la escala gráfica correspondiente.
|
|
|
|
|
2.- Primer Bloque
La recta r es la Directriz de las Parábolas que pasan
por los puntos P y Q :
1.- Determinar el Vértice, el Foco y el Eje de las
Parábolas.
2.- Dibuja las Parábolas utilizando 4 puntos.
|
|
|
|
|
3.- Primer Bloque
Dadas las vistas diédricas, dibuja en perspectiva
axonométrica isométrica la correspondiente figura
a escala 2 : 1.
No aplicar el coeficiente de reducción.
|
|
|
|
|
1.- Segundo bloque
La recta r contiene la arista de un tetraedro regular y
el punto M es el punto medio de la arista opuesta.
Determina sus proyecciones. Haz un croquis explicativo
de la solución.
|
|
|
|
|
|
EVALUACIÓN DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2017 (extraordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
Dibuja un ciclo del Hipocicloide que describe el punto
P de la circunferencia de centro O1 , y radio 25 mm
(RULETA), siendo la base la circunferencia de centro O2
y radio 75 mm.
|
|
|
|
|
2.- Primer Bloque
Dadas las vistas diédricas dibuja en Perspectiva
Axonométrica Isométrica la correspondiente figura
a escala 1 : 1. No aplicar el coeficiente de reducción
|
|
|
|
|
3.- Primer Bloque
Dada la perspectiva axonométrica isométrica a
escala 1 :1, se pide:
1) Dibujar, a escala NATURAL, EL ALZADO en
SEMICORTE.
2) ACOTAR, todo lo posible. Tomar las medidas
directamente de la ilustración. No aplicar el
coeficiente de reducción
|
|
|
|
|
1.- Segundo bloque
Los puntos A (25, 5, 40) y B (-5, 40, 70) definen el lado
de un pentágono regular.
1) Dibuja sus proyecciones sabiendo que el vértice
opuesto al lado AB tiene 30 mm de cota y el máximo
alejamiento posible.
2) Determina las trazas del plano que lo contiene.
|
|
|
|
|
1.- Primer Bloque
Construye la figura a escala 1 : 500.
a) AE = ED
b) AC = 40 metros
c) BC = 25 metros
d) CD = 50 metros
e) ángulo ACD = 90º
f) ángulo B = 90º
g) ángulo E = 135º
|
|
|
|
|
2.- Primer Bloque
1 - Dibuja el triángulo ABC con los siguientes datos:
AB = 80 mm
BC = 40 mm
Ángulo C = 22º 30'
2 - Dibuja la ELIPSE que pasa por el punto C , siendo
los puntos A y B sus focos.
3 - Dibuja un cuarto de la curva utilizando como
mínimo cuatro puntos.
|
|
|
|
|
3.- Primer Bloque
Dadas las vistas diédricas, dibuja en perspectiva
axonométrica isométrica la correspondiente
figura a escala 2 : 1.
No aplicar el coeficiente de reducción.
|
|
|
|
|
1.- Segundo bloque
Los puntos A (0, 50, 70) y M (30, 30, 40) definen la
altura de un triángulo equilátero contenido en un
plano proyectante horizontal.
1 - Dibuja las proyecciones del triángulo equilátero.
2 - Este triángulo es la cara de un octaedro regular.
Dibuja sus proyecciones.
El poliedro está en el primer cuadrante.
(Para la resolución del ejercicio se recomienda
utilizar un cambio de plano).
|
|
|
|
|
|
EVALUACIÓN DEL BACHILLERATO PARA EL ACCESO
A LA UNIVERSIDAD Junio 2018 (Ordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
1.- Dibuja el polígono ABCDE a escala 1 : 250 con los
siguientes datos:
AC = 22,5 metros
Altura sobre BC = 20 metros
Ángulo ABC = 60º
Ángulo ADC = 75º
CD = 10 metros
Ángulo AED = 135º
AE = 15 metros
2.- Dibuja la escala gráfica.
|
|
|
|
|
2.- Primer Bloque
Dada la figura en perspectiva Axonométrica Isométrica
a escala 1 : 1, se pide :
1.- Dibujar la vista frontal y el perfil a escala natural.
2.- Acotar.
Coger las medidas directamente del dibujo.
|
|
|
|
|
3.- Primer Bloque
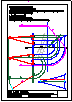
Los puntos F y E son los focos de una HIPÉRBOLA que
pasa por el punto Q. Realizar a escala 2:1 lo siguiente :
1) Determinar los ejes.
2) Dibuja las dos ramas de la HIPÉRBOLA utilizando
8 puntos como mínimo.
|
|
|
|
|
1.- Segundo bloque
Los puntos A(15, 85, 90) y M(-40, 40, 25) definen la
altura de un triángulo isósceles:
1 - El lado desigual pasa por el punto M y tiene un
vértice en el primer bisector con el mayor alejamiento
posible.
2 - El ángulo desigual del triángulo tiene un
ángulo de 30º.
3 - Dibuja las proyecciones del triángulo.
|
|
|
|
|
1.- Primer Bloque
Dadas las vistas diédricas, dibuja la PERSPECTIVA
AXONOMÉTRICA ISOMÉTRICA a escala 2 : 1.
Toma las medidas directamente del dibujo.
No utilizar el coeficiente de reducción.
|
|
|
|
|
2.- Primer Bloque
Conociendo el radio de la ruleta y los punto P, Q y
R, dibuja :
1.- Medio ciclo de la CICLOIDE correspondiente a la
ruleta de radio = 25 mm.
2.- La alargada de la CICLOIDE dado el punto Q.
3.- La acortada de la CICLOIDE dado el punto R.
|
|
|
|
|
3.- Primer Bloque
Dada la figura en perspectiva axonométrica isométrica
a escala 1 : 1, se pide:
1 - Representar la VISTA FRONTAL con la sección que
consideres adecuada a escala natural.
2 - ACOTAR todo lo posible.
Coger las medidas directamente del dibujo.
|
|
|
|
|
1.- Segundo bloque
Dado el plano a por los puntos A(-50, 0, 0), B(0, 50, 0) y
C(0, 0, 25). se pide:
1 - Situar en a un punto P de 25 mm de cota y 40 mm
de alejamiento.
2 - Dibujar las proyecciones del triángulo equilátero
inscrito en una circunferencia de centro el punto P
y radio 40 mm, el lado más bajo es paralelo al PH.
3 - Dibujar las proyecciones del TETRAEDRO que se
apoya por esta cara en el plano a. |
|
|
|
|
|
EVALUACIÓN DEL BACHILLERATO PARA EL ACCESO
A LA UNIVERSIDAD Junio 2018 (ExtraOrdinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
1.- Dado el croquis de la figura, se pide:
1.- Dibujar el plano a escala 1 : 250
2.- Construir la escala gráfica correspondiente.
|
|
|
|
|
2.- Primer Bloque
Dadas las vistas diédricas dibuja en Perspectiva
Axonométrica Isométrica la correspondiente figura
a escala 1 : 1. No aplicar el coeficiente de reducción.
|
|
|
|
|
3.- Primer Bloque
Los puntos A y B definen los focos de una ELIPSE que
pasa por el punto P.
1 - Determinar los ejes.
2 - Dibuja el cuadrante superior derecho utilizando
un mínimo de 4 puntos.
|
|
|
|
|
1.- Segundo bloque
Los puntos M (-60, 40, 50) y A (-10, 60, 80) definen
la altura de un TRIÁNGULO EQUILÁTERO. A es el
vértice y M el pie de la altura.
Dibuja sus proyecciones sabiendo que otro
vértice está lo más cerca posible del 2º bisector.
|
|
|
|
|
1.- Primer Bloque
Dadas las vistas diédricas, dibuja en PERSPECTIVA
AXONOMÉTRICA ISOMÉTRICA la correspondiente
figura a escala 2 : 1.
No aplicar el coeficiente de reducción coger las
medidas que faltan del dibujo.
|
|
|
|
|
2.- Primer Bloque
Dibuja una EPICICLOIDE con los siguientes datos.
Radio de la base = 40 mm Radio de la ruleta = 15 mm
|
|
|
|
|
3.- Primer Bloque
Dada la perspectiva axonométrica isométrica de la
ilustración a escala 1 : 1, se pide:
- Dibujar a escala natural, el ALZADO EN SEMICORTE.
Tomar las medidas directamente del dibujo.
|
|
|
|
|
1.- Segundo bloque
Dibuja las proyecciones de un HEXAEDRO REGULAR:
1 - El cuadrado ABCD es la base inferior del Hexaedro.
El punto C es contiguo al punto B, está en el PH y
tiene el mayor alejamiento posible. Datos
A(-40, 80, 40) y B(0, 60, 20).
2 - Dibuja las proyecciones del HEXAEDRO.
|
|
|
|
|
|
EVALUACIÓN DEL BACHILLERATO PARA EL ACCESO
A LA UNIVERSIDAD Junio 2019 (Ordinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
El punto F es el foco de una elipse y el segmento CD
es el eje menor:
1.- Determina el eje mayor de la elipse.
2.- Determina el punto P de la elipse que
dista 80 mm del foco F.
3.- Dibuja la recta tangente a la elipse en el puntyo P.
|
|
|
|
|
2.- Primer Bloque
Dibuja el polígono ABCDE a escala 1 : 500 :
1.- DATOS:
Triángulo ABC :
- AC = 50 metros
- Ángulo ABC = 120º
- AB = CB
Triángulo ADC :
- Mediana sobre AC = 40 metros
- CD = 35 metros
- Ángulo AED = 135º
Triángulo AED :
- Altura sobre AD = 30 metros
- Altura sobre DE = 50 metros
2.- Dibuja la escala gráfica.
|
|
|
|
|
3.- Primer Bloque
Dada la figura en perspectiva axonométrica isométrica
a escala 1 : 1, se pide:
1.- Representar la vista de alzado con el corte que
consideres adecuado a escala 1 : 1.
2.- Acotar todo lo posible.
Coger las medidas directamente del dibujo.
|
|
|
|
|
1.- Segundo bloque
A y B definen el lado de un triángulo equilátero.
Dibujar sus proyecciones.
Sabiendo que el tercer vértice está lo más a la
izquierda posible del plano de perfil que pasa por
el punto medio del lado AB.
|
|
|
|
|
1.- Primer Bloque
Dadas las vistas diédricas, dibuja la PERSPECTIVA
AXONOMÉTRICA ISOMÉTRICA a escala 1 : 1.
Para representar el arco utiliza el óvalo de 4 centros.
Obtener las medidas que faltan del dibujo.
No utilizar el coeficiente de reducción.
|
|
|
|
|
2.- Primer Bloque
Dadas las vistas de la ilustración, halla el alzado
correspondiente a escala 2 : 1. Toma las medidas
de las vistas dadas.
|
|
|
|
|
3.- Primer Bloque
Dados el punto Q, el punto P y la recta r, se pide:
- Dibujar las circunfeencias tangentes a la recta r
pasando por los puntos Q y P.
|
|
|
|
|
1.- Segundo Bloque
Los puntos A y B definen el lado más a la derecha de
un cuadrado contenido en un plano paralelo a la línea
de tierra.
Este cuadrado es la base donde se apoya un hexaedro
regular.
Dibujar las proyecciones del hexaedro.
|
|
|
|
|
|
EVALUACIÓN DEL BACHILLERATO PARA EL ACCESO
A LA UNIVERSIDAD Junio 2019 (EXTRAOrdinaria)
|
|
Enunciado
|
OPCIÓN A
|
OPCIÓN B
|
| |
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
DATOS Y
HOJA REALIZAR
|
SOLUCIÓN
|
1.- Primer Bloque
Dibuja el cuadrado equivalente a un triángulo
siguiendo los siguientes pasos:
1.- Dibuja el triángulo con los siguientes datos:
Lado AB = 80 mm
Vértice C = 120º
Lado AC = 30 mm
2.- Dibuja el rectángulo equivalente al triángulo ABC:
3.- Dibuja el cuadrado equivalente al rectángulo.
|
|
|
|
|
2.- Primer Bloque
Dada la figura en perspectiva axonométrica isométrica
a escala natural, se pide:
1.- Dibujar el ALZADO y la PLANTA a escala 1 : 1.
2.- ACOTAR las vistas.2.- ACOTAR las vistas.
|
|
|
|
|
3.- Primer Bloque
Sabiendo que la recta e es el eje de una parábola, d la
directriz y el punto C un punto de la parábola, se pide:
1.- Determinar el foco y el vértice de la parábola.
2.- Dibujar la parábola utilizando 8 puntos como mínimo.
|
|
|
|
|
1.- Segundo bloque
A y B definen el lado de un triángulo equilátero.
Dibujar sus proyecciones.
Sabiendo que el tercer vértice está lo más a la
izquierda posible del plano de perfil que pasa por
el punto medio del lado AB.
|
|
|
|
|
1.- Primer Bloque
Dadas las vistas diédricas a escala natural, dibuja
la PERSPECTIVA AXONOMÉTRICA ISOMÉTRICA
a escala 2 : 1.
Obtener las medidas del dibujo.
No utilizar el coeficiente de reducción.
|
|
|
|
|
2.- Primer Bloque
Dada la figura en perspectiva axonométrica
isométrica a escala 1 : 1, se pide:
1.- Representar el ALZADO con el corte que
consideres adecuado a escala natural.
2.- ACOTAR todo lo posible. Coger las medidas
directamente del dibujo.
|
|
|
|
|
3.- Primer Bloque
Dibuja el polígono ABCDE a escala 1 : 250 :
1.- DATOS: - AC 20 metros
- Altura sobre AC = 2,5 metros
- Ángulo ABC = 120º
- Altura sobre EC = 10 metros
- Altura sobre AE = 17,5 metros
- Ángulo EDC = 60º
- Altura sobre ED = 15 metros
2.- Dibuja la escala gráfica.
|
|
|
|
|
1.- Segundo Bloque
Los puntos A y B definen la diagonal principal
de un octaedro regular. Dibuja sus proyecciones
sabiendo que tiene un vértice en el primer
bisector a la menor cota posible.
|
|
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2020 (Ordinaria) |
|
Enunciado |
OPCIÓN ÚNICA |
| |
DATOS |
SOLUCIÓN
|
1.- Primer Bloque
Dibuja el polígono ABCDE a escala 1 : 250 :
1.- Dibuja la escala gráfica 1 : 250.
2.- Datos los del croquis.
Observaciones: la letra "h" hace referencia a la altura.
El lado ED es mayor que CD.
|
|
|
2.- Primer Bloque
Dada la figura en perspectiva axonométrica isométrica
a escala natural, se pide:
1.- Dibujar el alzado y la planta a escala 1 : 1.
2.- Acotar las vistas.
|
|
|
3.- Primer Bloque
Dadas las vistas de la ilustración, halla la vista del
alzado a escala 2 / 1. Toma las medidas de las vistas dadas.
|
|
|
4.- Primer Bloque
Dibuja un ciclo del Hipocicloide que describe el punto P
de la circunferencia de centro O1 , y radio 25 mm
(Ruleta), siendo la base la circunferencia de centro O2 , y
radio 75 mm.
|
|
|
1.- Segundo Bloque
Los puntos A( -50, 15, 15) y B(0, 60, 70) definen la
hipotenusa de un triángulo rectángulo. El pie de la
altura sobre la hipotenusa es el punto P(-20, Y, Z).
Se pide dibujar sus proyecciones sabiendo que el vértice
C está lo más a la derecha posible.
|
|
|
2.- Segundo Bloque
En los planos de perfil que distan entre sí 60 mm se
apoyan dos caras de un octaedro regular.
Dibujar la proyección vertical (EL ALZADO) y la
tercera proyección (PERFIL) sabiendo que el vértice
más bajo de la cara apoyada en el plano de la derecha,
tiene de cota 20 mm y el máximo alejamiento posible.
El centro del poliedro tiene de cota 50 mm.
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Julio 2020 (Extraordinaria) |
|
Enunciado |
OPCIÓN ÚNICA |
| |
DATOS |
SOLUCIÓN
|
1.- Primer Bloque
Dibuja el rectángulo equivalente a un pentágono
siguiendo los siguientes pasos:
1.- Dibuja el pentágono
conociendo su lado
AB = 40 mm.
2.- Dibuja el rectángulo equivalente.
|
|
|
2.- Primer Bloque
La recta e es el eje de la PARÁBOLA, F es el foco y C un
punto de la curva, se pide:
1.- Determinar el VÉRTICE y la DIRECTRIZ de la
PARÁBOLA.
2.- Dibujar la PARÁBOLA utilizando 8 puntos como
mínimo.
3.- Trazar la recta TANGENTE y la NORMAL en el
punto C.
|
|
|
3.- Primer Bloque
Dadas las vistas diédricas, dibuja la PERSPECTIVA
AXONOMÉTRICA ISOMÉTRICA a escala 2 : 1.
Obtener las medidas que faltan del dibujo.
No utilizar el coeficiente de reducción.
|
|
|
4.- Primer Bloque
Conociendo el radio de la ruleta y los puntos
P y Q , dibuja:
1 - Medio ciclo de la CICLOIDE correspondiente
a la ruleta
de radio = 25 mm.
2 - La ALARGADA de la CICLOIDE dado el punto Q.
|
|
|
1.- Segundo Bloque
El segmento AB es el lado de un CUADRADO cuyo
centro está lo más a la izquierda posible.
Dibuja sus proyecciones.
|
|
|
2.- Segundo Bloque
La diagonal principal AB de un HEXAEDRO mide
80 mm, es paralela a la Línea de Tierra y tiene
70 mm de cota. B queda a la derecha de A.
Dibujar el ALZADO o proyección vertical y el PERFIL
o tercera proyección sabiendo que el vértice más bajo
de los unidos con el vértice B, tiene cota 40 mm y el
máximo alejamiento posible.
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2021 (Ordinaria) |
|
Enunciado |
OPCIÓN ÚNICA |
| |
DATOS |
SOLUCIÓN
|
1.- Primer Bloque
Dadas las vistas diédricas. Dibuja la perspectiva axonométrica
isométrica a Escala 1 : 1.
No utilizar el coeficiente de reducción.
|
|
|
2.- Primer Bloque
Dibuja las circunferencias
tangentes a las rectas R y S, y
que
pasen por el punto P. |
|
|
3.- Primer Bloque
Dibuja un ciclo de Hipocicloide
con los siguientes datos:
1.-
Radio de la base = 90 mm.
2.-
Radio de la ruleta = 30 mm. |
|
|
4.- Primer Bloque
Los puntos F y E son los
focos de una Hipérbola que pasa
por
el punto Q.
Realiza
a escala 2 : 1 lo siguiente:
1.-
Determinar los ejes.
2.-
Dibujar las dos ramas de la Hipérbola utilizando 8 puntos
como
mínimo. |
|
|
1.- Segundo Bloque
Los puntos A( -60, 90, 20)
y M(0, 40, 20) definen la altura
de
un triángulo equilátero. Se pide:
1.-
Dibujar sus proyecciones sabiendo que el lado que pasa por
el
punto M, es paralelo al primer bisector.
2.-
Dibujar las trazas del plano que lo contiene. |
|
|
2.- Segundo Bloque
1.- Los puntos A(0, 10,
30) y B(50, 50, 30) definen el lado .
de
un triángulo equilátero contenido en un plano
Proyectante
Horizontal.
Dibuja
sus proyecciones.
2.-
Dibujar las proyecciones del Hexaedro regular situado
en
el primer cuadrante siendo los vértices del triángulo
vértices
del Hexaedro. |
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2021 (ExtraOrdinaria) |
|
Enunciado |
OPCIÓN ÚNICA |
1.- Primer Bloque
Dibuja medio ciclo de la
Cicloide que describe el punto P de
la
circunferencia de centro O , y radio 20 mm. (Ruleta) |
|
|
2.- Primer Bloque
Dibuja el polígono ABCDE
a escala 1 : 500 :
1.-
Dibuja la Escala Gráfica 1 : 500.
2.-
Datos los del croquis.
Deben
de quedar claras las construcciones geométricas que
sean
necesarias para la construcción de los triángulos. |
|
|
3.- Primer Bloque
Dada la PERSPECTIVA AXONOMÉTRICA
ISOMÉTRICA
de la pieza
a escala 1 : 2, se pide:
1.-
Dibujar, a escala NATURAL, el alzado con el corte
más
apropiado.
2.-
Acotar todo lo posible.
Obtener
las medidas del dibujo.
No
utilizar el coeficiente de reducción. |
|
|
4.- Primer Bloque
Dadas las vistas diédricas,
dibuja la PERSPECTIVA
AXONOMÉTRICA
ISOMÉTRICA a escala 2 : 1.
Obtener
las medidas del dibujo.
No
utilizar el coeficiente de reducción. |
|
|
1.- Segundo Bloque
Dada la recta R, definida
por los puntos A(-15, 15, 0) y
B(-38,
0, -15) y el punto P(0, 51, 36), se pide:
Dibujar
las proyecciones del CUADRADO que tiene un
lado
en la recta R, siendo el punto P su centro. |
|
|
2.- Segundo Bloque
Dada la recta R, definida por los puntos A(-15, 15, 0) y
B(-38, 0, -15) y el punto P(0, 51, 36), se pide:
Dibujar las proyecciones del CUADRADO que tiene un
lado en la recta R, siendo el punto P su centro.
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2022 (Ordinaria) |
|
Enunciado |
OPCIÓN ÚNICA |
1.- Primer Bloque
Dadas las vistas diédricas.
Dibuja la perspectiva axonométrica
isométrica
a Escala 2 : 1.
Obtener
las medidas del dibujo.
No
utilizar el coeficiente de reducción. |
|
|
2.- Primer Bloque
Dibuja el polígono ABCDE
a Escala 1 : 250.
Dibuja
la Escala Gráfica 1 : 250.
Datos
los del croquis. |
|
|
3.- Primer Bloque
Dadas las vistas de la ilustración, halla el ALZADO
correspondiente a la dirección señalada a Escala 2 / 1.
Toma las medidas de las vistas dadas.
|
|
|
4.- Primer Bloque
Dadas las vistas de la ilustración, halla el ALZADO
correspondiente a la dirección señalada a Escala 2 / 1.
Toma las medidas de las vistas dadas.
|
|
|
1.- Segundo Bloque
Los puntos A( 0, 15, 30) y B(-60, 80, 30) definen la diagonal
de un cuadrado. Se pide:
1.- Dibujar sus proyecciones sabiendo que la otra diagonal es
paralela al primer bisector.
2.- Dibujar las trazas del plano que contiene al cuadrado.
|
|
|
2.- Segundo Bloque
El punto A( 0, 20, 35) es el vértice de un triángulo equilátero
de vértices ABC.
El lado opuesto al vértice A está situado en la recta
R(P(55, 0, 20); Q(10, 85, 70)).
Este triángulo es la cara de un tetraedro regular de vértices
ABCD, se pide:
Determinar las proyecciones del poliedro sabiendo que el
vértice D se encuentra lo más alto posible.
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2022 (ExtraOrdinaria) |
|
Enunciado |
OPCIÓN ÚNICA |
1.- Primer Bloque
Dada la figura en perspectiva axonométrica isométrica a
Escala 1 : 1, se pide:
Representar el ALZADO con un corte a escala 2 : 1.
Coger las medidas directamente del dibujo.
No utilizar el coeficiente de reducción.
|
|
|
2.- Primer Bloque
Dibuja el polígono ABCDE a Escala 1 : 250.
1.- Con los siguientes datos:
Triángulo ABC:
- AC = 25 metros
- Ángulo B = 105º
- Ángulo C = 45º
Triángulo ADC:
- Altura sobre CD = 20 metros
- Altura sobre AD = 15 metros
Triángulo AED:
- Ángulo AED = 120º
- Altura sobre AE = 10 metros
|
|
|
3.- Primer Bloque
Dados el punto Q, el punto P y la recta r, se pide:
Dibujar las circunferencias tangentes a la recta r
pasando por los puntos Q y P.
|
|
|
4.- Primer Bloque
El punto F es el foco de una HIPÉRBOLA y el segmento CD
es el eje menor:
1.- Determinar el eje mayor de la HIPÉRBOLA.
2.- Determinar el punto P de la HIPÉRBOLA que dista 30 mm
del foco F.
3.- Dibuja la tangente a la HIPÉRBOLA en el punto P.
|
|
|
1.- Segundo Bloque
Los puntos A(-30, 10, 10) y B(20, 40, 50) definen el lado desigual
de un de un triángulo isósceles de vértices ABC. Dibuja sus
proyecciones sabiendo que:
1.- La altura del vértice C mide 45 mm.
2.- El vértice C tiene el mismo alejamiento que el punto B y
se encuentra situado lo más a la izquierda posible.
|
|
|
2.- Segundo Bloque
Los puntos A( -50, 30, 30) y B(-35. 60. 15) definen el lado de un
cuadrado de vértices ABCD.
proyecciones sabiendo que:
1.- Dibuja las proyecciones del cuadrado sabiendo que el vértice C,
situado junto al vértice B, se encuentra a una cota de 30 mm y con.
el mayor alejamiento posible.
2.- Este cuadrado es la base de un HEXAEDRO regular. Los otros
cuatro vértices del HEXAEDRO están situados lo más alto posible.
Dibujar sus proyecciones.
|
|
|