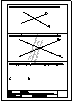
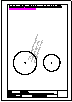
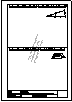
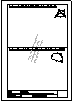
Ejercicios para resolver. Geometría
Métrica
1.- Hallar el lugar geométrico de los puntos medios de las
cuerdas de una determinada circunferencia ( radio= 45 mm ), que tengan
una longitud dada ( cuerda = 60 mm ).
una longitud dada ( cuerda = 60 mm ).
2.- Construir un triángulo conocido el lado a = 75 mm, su ángulo
opuesto  = 50° y la relación entre los lados b / c = 3 / 4.
3.- Construir un triángulo conocido el lado a = 120 mm, la altura
correspondiente a este lado ha = 55 mm y el lado b = 70 mm.
4.- Construir un triángulo isósceles, ángulo desigual en A, conocido
el ángulo  = 50° y la altura ha = 70 mm.
5.- Construir un triángulo isósceles, ángulo desigual en A, conocido
el lado a = 90 mm y la mediana mb = 75 mm.
6.- Construir un triángulo conocido el lado a = 50 mm, la suma de
los otros dos b+c = 80 mm y el ángulo  = 60°
= 60°
7.- Construir un triángulo conocido el lado a = 50 mm, el ángulo
opuesto  = 60° y la altura corespondiente al lado c, hc = 35 mm.
8.- Construir un triángulo conociendo su perímetro 2p = 100 mm y
dos ángulos  = 60° y
= 60° y  = 45°.
= 45°.
9.- Construir un trapecio conocidos los cuatro lados B = 90 mm,
b = 60 mm, L = 50 mm y l = 45 mm.
10.- Construir un rectángulo conocida la suma de los lados a + b
= 100 mm y el ángulo que forman las diagonales  = 120°.
11.- Construir un romboide conocido el lado a = 37.5 mm, el ángulo
que forman las diagonales  = 80° y la diferencia entre las
diagonales D - d = 15 mm.
diagonales D - d = 15 mm.
12.- Construir un triángulo conocido su perímetro
= 115 mm, el ángulo  = 50° y la altura hc = 40 mm
13.- Construir un triángulo conocido su perímetro
= 115 mm, el ángulo  = 45° y la altura ha = 40 mm
14.- Construir un triángulo conocido el lado a = 70 mm, el
ángulo opuesto  = 60° y el punto P, perteneciente a la bisectriz
del ángulo Â, que
dista 36 mm del vértice B y 54 mm del vértice C.
dista 36 mm del vértice B y 54 mm del vértice C.
15.- Construir un triángulo sabiendo que la diferencia entre
los lados a y c es de 15 mm, el ángulo  = 45° y que el lado b mide = 50 mm
= 45° y que el lado b mide = 50 mm
16.- Construir un triángulo conocido el radio de la circunferencia
circunscrita = 32mm, el radio de la circunferencia inscrita = 14 mm y
un ángulo  = 60°.
17.- Determinar el cuarto vértice de un cuadrilátero
ABCD del que conocemos AB = 45 mm, BC = 50 mm y el radio de la circunferencia
circunscrita = 35 mm para que este cuadrilátero sea inscriptible en la circunferencia dada y circunscriptible a otra circunferencia.
Determinar, también, el radio de ésta.
circunscrita = 35 mm para que este cuadrilátero sea inscriptible en la circunferencia dada y circunscriptible a otra circunferencia.
Determinar, también, el radio de ésta.
18.- Determinar un cuadrado del que se conoce la diferencia entre
la diagonal y el lado. D-L = 25 mm.
19.- Determinar un paralelogramo del que conocemos sus diagonales
AC = 85 mm, BD = 50 mm y el ángulo  = 45°
20.- Determinar un paralelogramo del que conocemos sus lados AB
= 40 mm, BC = 50 mm y el ángulo entre sus diagonales a
= 105°
21.- Determinar un paralelogramo del que conocemos la diferencia
entre sus diagonales D - d = 30 mm, el ángulo entre sus diagonales
a = 135° y el
lado menor a = 45 mm.
lado menor a = 45 mm.
22.-
Determinar un cuadrilátero circunscriptible e inscriptible.
23.-
Resolver figura utilizando tangencias. Aplicación de potencia, ejes y
centros radicales.
24.-
Resolver figuras semejantes. Aplicación de homotecia y semejanza.
25.-
Ejercicios sobre potencia.
26.-
Ejercicios sobre afinidad.
27.-
Ejercicios sobre cónicas.
28.-
Ejercicio sobre perspectiva cónica central.
29.-
Ejercicio sobre perspectiva cónica central.
30.-
Ejercicio sobre perspectiva cónica 2 fugas.
31.-
Ejercicio sobre perspectiva cónica 2 fugas.
32.- Determinar un triángulo cuyo lado mide 85 mm, su ángulo opuesto
mide 50° y los otros dos lados están en relación 4 / 3.
33.- Determinar un triángulo cuyos lados b y c miden 85mm y 45 mm,
respectivamente, y la mediana correspondiente al otro lado mide 60 mm.
34.-
Dados dos triángulos ABC dividir en 3 el primero y en 5 partes el segundo,
de igual área.
35.-
Construir un triángulo conocidos los siguientes datos: ma
= 60 mm, m b = 75 mm y ha
= 50 mm .
Construir un triángulo conocidos los siguientes datos: m a = 65 mm, ha = 58 mm y hb = 60mm.
Construir un triángulo conocidos los siguientes datos: m a = 65 mm, ha = 58 mm y hb = 60mm.
36.-
Construir un triángulo conocidos los siguientes datos: ma
= 56 mm, ha = 48 mm y  = 75º.
Construir un triángulo conocidos los siguientes datos: b = 50 mm, a + c = 100 mm y  =75º.
Construir un triángulo conocidos los siguientes datos: b = 50 mm, a + c = 100 mm y  =75º.
37.-
Determinar los elementos de la homología necesarios, para obtener la cónica
definida por los puntos A, B, C, D y E.
38.-
Obtener, gráficamente, la siguiente expresión. 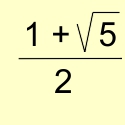 (Tomar como unidad 20mm).
(Tomar como unidad 20mm).
Obtener la rectificación de la circunferencia dada. Método de Specht.
Obtener la rectificación de la circunferencia dada. Método de Specht.
39.-
Enlazar, mediante arcos del mismo sentido y distinto radio, dos rectas
paralelas conocidos los puntos de tangencia.
Obtener los ejes reales de una elipse conocidos dos diámetros conjugados.
Obtener los ejes reales de una elipse conocidos dos diámetros conjugados.
40.-
Dibujar a escala 2,5 : 1, la pieza dada. Solucionar todos los casos de
tangencias necesarios.
41.-
Determinar un heptadecágono regular inscrito en una circunferencia de
radio = 80mm. (Construcción particular).
(Se utilizará, preferentemente el método de Gauss - Richmond).
(Se utilizará, preferentemente el método de Gauss - Richmond).
42.-
Determinar todos los elementos de la elipse, incluida la cónica, definida
por el eje mayor AB y la tangente t.
Determinar todos los elementos de la elipse, incluida la cónica, definida por el eje menor CD y la tangente t.
Determinar todos los elementos de la elipse, incluida la cónica, definida por el eje menor CD y la tangente t.
43.-
Dibujar la pieza dada a escala 3 : 4. Solucionar todos los casos de tangencias
necesarios.
44.-
Construir un triángulo conocidos los siguientes elementos:
h a = 85 mm, h b = 60 mm y el ángulo que forma la mediana (m a ) con el lado b = 20º.
Construir un triángulo conocidos los siguientes elementos:
Radio de la circunferencia inscrita (r i ) = 20 mm, radio de la circunferencia exinscrita (r a ) = 40mm y la diferencia entre los lados
c y b ( c - b ) = 15mm.
h a = 85 mm, h b = 60 mm y el ángulo que forma la mediana (m a ) con el lado b = 20º.
Construir un triángulo conocidos los siguientes elementos:
Radio de la circunferencia inscrita (r i ) = 20 mm, radio de la circunferencia exinscrita (r a ) = 40mm y la diferencia entre los lados
c y b ( c - b ) = 15mm.
45.-
Construir un triángulo conocidos los siguientes elementos:
m a = 60 mm, m b = 65 mm y el ángulo ( ) = 55º.
) = 55º.
Construir un triángulo conocidos los siguientes elementos:
Perímetro (2p) = 220mm, el ángulo ( Â ) =30º y la altura correspondiente al lado b ( h b ) = 40mm.
m a = 60 mm, m b = 65 mm y el ángulo (
Construir un triángulo conocidos los siguientes elementos:
Perímetro (2p) = 220mm, el ángulo ( Â ) =30º y la altura correspondiente al lado b ( h b ) = 40mm.
46.-
Construir un triángulo conocidos los siguientes elementos:
La altura correspondiente al lado a ( h a ) = 50 mm, la mediana correspondiente al lado a ( m a) = 60 mm y la bisectriz
correspondiente al ángulo  ( V a ) = 55mm .
Construir un trapecio conocidos los siguientes elementos:
La base mayor (B) mide 70 mm, la base menor (b) mide 50 mm y las diagonales miden 75 y 85 mm .
La altura correspondiente al lado a ( h a ) = 50 mm, la mediana correspondiente al lado a ( m a) = 60 mm y la bisectriz
correspondiente al ángulo  ( V a ) = 55mm .
Construir un trapecio conocidos los siguientes elementos:
La base mayor (B) mide 70 mm, la base menor (b) mide 50 mm y las diagonales miden 75 y 85 mm .
47.-
Construir un triángulo conocidos los siguientes elementos:
La hipotenusa está sobre la recta r. Los catetos o sus prolongaciones pasan por los puntos P y Q. La altura correspondiente
a la hipotenusa (h a ) mide = 40mm .
Construir un trapecio conocidos los siguientes elementos:
El radio de la circunferencia circunscrita (R) mide 55mm, uno de los lados no paralelos (L) mide 70 mm y la altura (h) mide 65 mm .
La hipotenusa está sobre la recta r. Los catetos o sus prolongaciones pasan por los puntos P y Q. La altura correspondiente
a la hipotenusa (h a ) mide = 40mm .
Construir un trapecio conocidos los siguientes elementos:
El radio de la circunferencia circunscrita (R) mide 55mm, uno de los lados no paralelos (L) mide 70 mm y la altura (h) mide 65 mm .
48.-
Construir un triángulo conocidos los siguientes elementos:
El lado (a) mide 50mm, el ángulo ( Â ) mide 30º y el radio de la circunferencia exinscrita ( ra ) mide 30 mm.
El lado (a) mide 50mm, el ángulo ( Â ) mide 30º y el radio de la circunferencia exinscrita ( ra ) mide 30 mm.
49.-
Construir un triángulo conocidos los siguientes elementos:
El ángulo ( Â ) mide 30º, los lados b y c ( b / c ) están en relación 4 / 3 y el perímetro ( 2p ) mide 180 mm.
Construir un triángulo conocidos los siguientes elementos:
Los lados b y c se encuentran sobre las rectas r y s. El punto P corresponde al final de la mediana ( ma) .
El ángulo ( Â ) mide 30º, los lados b y c ( b / c ) están en relación 4 / 3 y el perímetro ( 2p ) mide 180 mm.
Construir un triángulo conocidos los siguientes elementos:
Los lados b y c se encuentran sobre las rectas r y s. El punto P corresponde al final de la mediana ( ma) .
50.-
Construir un cuadrilátero inscriptible ABCD conocidos los siguientes elementos:
La diagonal ( AC ) mide 80mm, el ángulo ( Â ) mide 60º, el ángulo que forma la diagonal BD con el lado AB es de 75º y la
relación entre el lado AB y el BC (AB / BC) es igual a 2.
Construir un cuadrilátero inscriptible ABCD conocidos los siguientes elementos:
Los puntos dados A, B, C y la suma de los lados ( CD + DA ) mide 112 mm.
La diagonal ( AC ) mide 80mm, el ángulo ( Â ) mide 60º, el ángulo que forma la diagonal BD con el lado AB es de 75º y la
relación entre el lado AB y el BC (AB / BC) es igual a 2.
Construir un cuadrilátero inscriptible ABCD conocidos los siguientes elementos:
Los puntos dados A, B, C y la suma de los lados ( CD + DA ) mide 112 mm.
51.-
Construir un triángulo conocidos los siguientes elementos:
El lado (a) mide 80 mm, el radio de la circunferencia inscrita (r) mide 20 mm y el radio de la circunferencia exinscrita
correspondiente al lado a (ra ) mide 70 mm.
El lado (a) mide 80 mm, el radio de la circunferencia inscrita (r) mide 20 mm y el radio de la circunferencia exinscrita
correspondiente al lado a (ra ) mide 70 mm.
52.-
Construir un triángulo conocidos los siguientes elementos:
El lado (a) mide 60 mm, el ángulo opuesto ( Â ) mide 40º y la diferencia entre los otros dos lados ( b - c ) mide 24 mm.
Construir un triángulo conocidos los siguientes elementos:
El lado (a) mide 75 mm, el radio de la circunferencia circunscrita ( R ) mide 50 mm y la suma de los cuadrados de los otros
dos lados ( b2 + c2 ) es de 12100.
El lado (a) mide 60 mm, el ángulo opuesto ( Â ) mide 40º y la diferencia entre los otros dos lados ( b - c ) mide 24 mm.
Construir un triángulo conocidos los siguientes elementos:
El lado (a) mide 75 mm, el radio de la circunferencia circunscrita ( R ) mide 50 mm y la suma de los cuadrados de los otros
dos lados ( b2 + c2 ) es de 12100.
53.-
Determinar los puntos de intersección de la recta r con la cónica definida
por los siguientes elementos.
Centro de la cónica, punto O, excentricidad = 0,75, semieje mayor a = 32 mm.
Centro de la cónica, punto O, excentricidad = 0,75, semieje mayor a = 32 mm.
54.-
Los puntos O y O´ son, respectivamente, los centros de una circunferencia
y una elipse afines de eje de afinidad la recta e.
Siendo la recta t´una tangente a la elipse, determinar los ejes de la cónica.
Una vez obtenidos los ejes construir, por haces proyectivos, la cónica.
Siendo la recta t´una tangente a la elipse, determinar los ejes de la cónica.
Una vez obtenidos los ejes construir, por haces proyectivos, la cónica.
55.-
Dibujar a escala 1 : 1 el contorno cuyo croquis, DEFORMADO, se acompaña.
Resolver todas las tangencias necesarias.
Resolver todas las tangencias necesarias.
56.-
Obtener las circunferencias tangentes dos a dos, conociendo sus centros
O1, O2, O3
.
Dado un cuadrado de 70 mm de lado obtener, gráficamente, un rectángulo equivalente a él sabiendo que uno de los lados del
rectángulo mide 50 mm.
Dado un cuadrado de 70 mm de lado obtener, gráficamente, un rectángulo equivalente a él sabiendo que uno de los lados del
rectángulo mide 50 mm.
57.-
Obtener un romboide conocido el lado AB = 40mm, el lado BC = 50mm y el
ángulo que forman las diagonales a = 105º
.
Obtener un romboide conocido el lado AB = 42mm, la diferencia entre las diagonales D - d = 56 mm y el ángulo que
forman éstas a = 135º.
Obtener un romboide conocido el lado AB = 42mm, la diferencia entre las diagonales D - d = 56 mm y el ángulo que
forman éstas a = 135º.
58.-
Obtener las circunferencias, que pasando por el punto P, son tangentes
a las dadas O1 y O2 .
Obtener las circunferencias, que pasando por el punto P, son tangentes a la recta r dada y a la circunferencia de centro O1.
Obtener las circunferencias, que pasando por el punto P, son tangentes a la recta r dada y a la circunferencia de centro O1.
59.-
Obtener un triángulo conocidas las medianas ma
, mb y la altura hc.
ma = 90 mm, mb = 66 mm, hc = 75 mm .
Obtener un triángulo conocidos los radios ra y rb , de las circunferencias exinscritas y la suma de los lados a + b .
ra = 15 mm, rb = 30 mm, a + b = 100 mm .
ma = 90 mm, mb = 66 mm, hc = 75 mm .
Obtener un triángulo conocidos los radios ra y rb , de las circunferencias exinscritas y la suma de los lados a + b .
ra = 15 mm, rb = 30 mm, a + b = 100 mm .
60.-
Obtener un triángulo conocidas las medianas ma
, mb y el ángulo  .
.
ma = 75 mm, mb = 66 mm, =
50º.
=
50º.
Obtener un triángulo conocidos el radio r de la circunferencia inscrita, el semiperímetro y el ángulo Â.
r = 20 mm, p = 120 mm, Â = 40º.
ma = 75 mm, mb = 66 mm,
Obtener un triángulo conocidos el radio r de la circunferencia inscrita, el semiperímetro y el ángulo Â.
r = 20 mm, p = 120 mm, Â = 40º.
61.-
Determinar los elementos principales de una hipérbola conocidos sus focos
y la recta r, tangente a ella. Una vez
determinados los elementos trazar la cónica y obtener el punto de tangencia entre la cónica y la recta dada.
determinados los elementos trazar la cónica y obtener el punto de tangencia entre la cónica y la recta dada.
62.-
De una parábola se conoce la distancia 2a = 56 mm, entre el foco y la
directriz, así como la posición de su eje principal
y del foco. Determinar los puntos de corte con la cónica de una recta, que pasando por el punto A forma 45º con el eje.
El vértice de la parábola se encuentra a la izquierda del foco.
No realizar el trazado de la cónica.
y del foco. Determinar los puntos de corte con la cónica de una recta, que pasando por el punto A forma 45º con el eje.
El vértice de la parábola se encuentra a la izquierda del foco.
No realizar el trazado de la cónica.
63.-
Obtener un triángulo conocidos los radios rb
y rc, de las circunferencias exinscritas y la diferencia
de los ángulos C y B ( -
-
 ).
).
rb = 10 mm, rc = 40 mm, -
-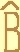 = 40º.
= 40º.
rb = 10 mm, rc = 40 mm,
Obtener un triángulo conocidos los radios rb y rc, de las circunferencias exinscritas y el lado a.
rb = 30 mm, rc = 25 mm y el lado a = 110 mm.
64.-
Obtener un triángulo conocidos los radios r y ra,
de las circunferencias inscrita y exinscritas y el ángulo Â.
r = 25 mm, ra = 40 mm, Â = 45º.
r = 25 mm, ra = 40 mm, Â = 45º.
Obtener el mayor de los triángulos conocido el lado c, el ángulo  y la relación entre el lado b y el lado a.
lado c = 50 mm, Â = 35º y b / a = 5 / 3.
65.-
Dibujar a escala 1 : 1 la figura propuesta, resolviendo todos los ejercicios
de tangencias necesarios.
66.-
Determinar un trapecio (A, C, D, E) conocidos los siguientes elementos.
Suma de sus bases = 120 mm, la diagonal d1 = 64 mm, la
diagonal d2 = 72 mm y el lado L1 = 36 mm.
De una parábola se conoce la distancia 2a = 45 mm, entre el foco y la directriz, así cómo la posición horizontal de su eje principal.
Determinar los puntos de corte con la cónica de una recta, que pasando por el punto A forma 45º con el eje.
Sin realizar el trazado de la cónica.
diagonal d2 = 72 mm y el lado L1 = 36 mm.
De una parábola se conoce la distancia 2a = 45 mm, entre el foco y la directriz, así cómo la posición horizontal de su eje principal.
Determinar los puntos de corte con la cónica de una recta, que pasando por el punto A forma 45º con el eje.
Sin realizar el trazado de la cónica.
67.-
Los puntos O y O´son, respectivamente, los centros de una circunferencia
y una elipse afines de eje de afinidad la recta e.
Siendo la recta t´una tangente a la elipse, determinar sus ejes reales y construir por haces proyectivos la cónica.
Siendo la recta t´una tangente a la elipse, determinar sus ejes reales y construir por haces proyectivos la cónica.
68.-
Determinar un triángulo acutángulo (A, B, C) conocidos los siguientes
elementos.
a = 90 mm, ha = 90 mm, mb = 70 mm.
Determinar un triángulo (A, B, C) conocidos los siguientes elementos.
ma = 90 mm, mb = 108 mm, hc = 72mm.
a = 90 mm, ha = 90 mm, mb = 70 mm.
Determinar un triángulo (A, B, C) conocidos los siguientes elementos.
ma = 90 mm, mb = 108 mm, hc = 72mm.
69.-
Determinar un triángulo conocidos los siguientes elementos.
c = 60 mm, b = 72 mm y ha = 36mm.
Dado un cuadrado de 70 mm de lado, construir un rectángulo equivalente a él, uno de cuyos lados mide 55 mm.
c = 60 mm, b = 72 mm y ha = 36mm.
Dado un cuadrado de 70 mm de lado, construir un rectángulo equivalente a él, uno de cuyos lados mide 55 mm.
70.-
Dibujar a escala 3 : 2 el contorno cuyo croquis se acompaña.
Resolver todas las tangencias necesarias.
Indicar, claramente, todos los centros y puntos de tangencia.
Resolver todas las tangencias necesarias.
Indicar, claramente, todos los centros y puntos de tangencia.
71.-
Dibujar a escala 3 : 2 el contorno cuyo croquis se acompaña.
Resolver todas las tangencias necesarias.
Indicar, claramente, todos los centros y puntos de tangencia.
Resolver todas las tangencias necesarias.
Indicar, claramente, todos los centros y puntos de tangencia.
72.-
Construir un cuadrilátero conocidos sus cuatro lados, sabiendo que el
segmento MN determina los puntos medios
de los lados AD y BC.
AB = 65 mm, BC = 105 mm, CD = 110 mm, DA = 70 mm.
Construir un cuadrilátero conocidos dos lados opuestos y sus cuatro ángulos.
AB = 80 mm, CD = 95 mm, Â = 105º,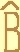 = 85º,
= 85º,  = 70º,
= 70º,  = 100º
= 100º
de los lados AD y BC.
AB = 65 mm, BC = 105 mm, CD = 110 mm, DA = 70 mm.
Construir un cuadrilátero conocidos dos lados opuestos y sus cuatro ángulos.
AB = 80 mm, CD = 95 mm, Â = 105º,
73.-
Construir un triángulo conocidas la mediana ma,
la altura ha y la relación entre los lados
a y b.
ma = 65 mm, ha= 62mm, b / a = 3 / 2.
Construir un triángulo conocidas las tres alturas.
ha = 65 mm, hb = 80mm y hc = 70 mm.
ma = 65 mm, ha= 62mm, b / a = 3 / 2.
Construir un triángulo conocidas las tres alturas.
ha = 65 mm, hb = 80mm y hc = 70 mm.
74.-
Construir un triángulo conocidas las tres medianas ma,
mb y mc.
ma = 66 mm, mb = 60 mm, mc = 72 mm.
Construir un triángulo conocidos los siguientes elementos el perímetro (2p) el ángulo  y la relación entre los
lados c y a (c / a). 2p = 170 mm, Â = 40º y c / a = 1,5.
ma = 66 mm, mb = 60 mm, mc = 72 mm.
Construir un triángulo conocidos los siguientes elementos el perímetro (2p) el ángulo  y la relación entre los
lados c y a (c / a). 2p = 170 mm, Â = 40º y c / a = 1,5.
75.-
Construir un triángulo conocidos los siguientes elementos el ángulo
 el radio de la circunferencia inscrita (r) y la
longitud de la bisectriz correspondiente al ángulo  (Va) .  = 50º, r = 25 mm, Va = 90 mm.
Construir un triángulo conocidos los siguientes elementos la longitud de la bisectriz (Va) la diferencia entre los ángulos
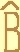 y
y  y la relación entre la
suma de los lados b y c y el lado a [(b + c) / a]. Va = 50
mm,
y la relación entre la
suma de los lados b y c y el lado a [(b + c) / a]. Va = 50
mm, 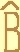 -
-  = 30º y (b + c) / a = 1,75
= 30º y (b + c) / a = 1,75
longitud de la bisectriz correspondiente al ángulo  (Va) .  = 50º, r = 25 mm, Va = 90 mm.
Construir un triángulo conocidos los siguientes elementos la longitud de la bisectriz (Va) la diferencia entre los ángulos
76.-
Realizar la figura siguiente, resolviendo los diferentes trazados de tangencias
que se presentan. Dejar los trazados auxiliares.
Indicar, claramente, los centros y puntos de tangencia. Escala 3 : 2.
Indicar, claramente, los centros y puntos de tangencia. Escala 3 : 2.
77.-
Realizar la figura siguiente, resolviendo los diferentes trazados de tangencias
que se presentan. Dejar los trazados auxiliares.
Indicar, claramente, los centros y puntos de tangencia.
Indicar, claramente, los centros y puntos de tangencia.
78.-
Realizar la figura siguiente, resolviendo los diferentes trazados de tangencias
que se presentan. Dejar los trazados auxiliares.
Indicar, claramente, los centros y puntos de tangencia.
Escala 3 : 4 la figura dada. Obtener, previamente, la escala gráfica.
Indicar, claramente, los centros y puntos de tangencia.
Escala 3 : 4 la figura dada. Obtener, previamente, la escala gráfica.
79.-
Realizar la figura siguiente, resolviendo los diferentes trazados de tangencias
que se presentan. Dejar los trazados auxiliares.
Indicar, claramente, los centros y puntos de tangencia.
Escala 5 : 6 la figura dada. Obtener, previamente, la escala gráfica.
Indicar, claramente, los centros y puntos de tangencia.
Escala 5 : 6 la figura dada. Obtener, previamente, la escala gráfica.
80.-
Determinar un punto interior al triángulo ABC de tal manera que las distancias
a los vértices estén relacionadas
según las siguientes proporciones. m / n = 1 / 2.75, m / p = 1 / 2.5 y p / n = 2.5 / 2.75.
según las siguientes proporciones. m / n = 1 / 2.75, m / p = 1 / 2.5 y p / n = 2.5 / 2.75.
81.-
Determinar los puntos del plano desde los cuales las tangentes a dos circunferencias
dadas midan 50 mm.
Una vez obtenidos los puntos trazar las tangentes a las dos circunferencias dadas.
Determinar los puntos del plano desde los cuales las dos circunferencias dadas se vean bajo un ángulo de 60º.
Una vez obtenidos los puntos trazar las tangentes a las dos circunferencias dadas.
Una vez obtenidos los puntos trazar las tangentes a las dos circunferencias dadas.
Determinar los puntos del plano desde los cuales las dos circunferencias dadas se vean bajo un ángulo de 60º.
Una vez obtenidos los puntos trazar las tangentes a las dos circunferencias dadas.
82.-
Determinar un cuadrilátero inscriptible conocido el lado AB = 50 mm, el
ángulo 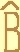 = 120º y las diagonales
L1 = 72 mm y
= 120º y las diagonales
L1 = 72 mm y
L2 = 80 mm.
Determinar un cuadrilátero inscriptible conocido el ángulo  = 75º el ángulo ABD = 40º y las diagonales L1 = 72 mm y
L2 = 80 mm.
L2 = 80 mm.
Determinar un cuadrilátero inscriptible conocido el ángulo  = 75º el ángulo ABD = 40º y las diagonales L1 = 72 mm y
L2 = 80 mm.
83.-
Determinar un triángulo rectángulo conocido el perímetro 2p = 200 mm y
la altura correspondiente a la hipotenusa
h a = 35 mm.
h a = 35 mm.
84.-
Determinar un triángulo conocido el radio de la circunferencia inscrita
r = 20 mm, el radio de la circunferencia
circunscrita R = 50 mm y el radio de una de las circunferencias exinscritas ra = 70 mm.
circunscrita R = 50 mm y el radio de una de las circunferencias exinscritas ra = 70 mm.
85.-
Dado un rectángulo de 50 mm de base y 30 mm de altura determinar un rectángulo
circunscrito. Cada vértice del
rectángulo dado estará sobre un lado del cuadrado, buscado. La diagonal del rectángulo buscado forma 40º con la
base y 50º con la altura.
Dado un rectángulo de 70 mm de base y 30 mm de altura determinar un rectángulo circunscrito. Cada vértice del
rectángulo dado estará sobre un lado del cuadrado, buscado. La diagonal del rectángulo buscado forma 30º con la
base y 60º con la altura.
rectángulo dado estará sobre un lado del cuadrado, buscado. La diagonal del rectángulo buscado forma 40º con la
base y 50º con la altura.
Dado un rectángulo de 70 mm de base y 30 mm de altura determinar un rectángulo circunscrito. Cada vértice del
rectángulo dado estará sobre un lado del cuadrado, buscado. La diagonal del rectángulo buscado forma 30º con la
base y 60º con la altura.
86.-
Cuadrilátero inscriptible conocidos sus cuatro lados :
a = 40 mm
b = 60 mm
c = 80 mm
d = 75 mm
a = 40 mm
b = 60 mm
c = 80 mm
d = 75 mm
87.-
Determinar un triángulo conocido un lado, la altura correspondiente a
dicho lado y la diferencia de los ángulos adyacentes.
Lado a = 60mm, la altura ha = 50mm y la diferencia de los ángulos B y C (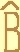 -
- )=
40º.
)=
40º.
Determinar un triángulo conocido un lado, la altura y la mediana correspondientes a dicho lado.
Lado a = 100 mm, la altura ha = 80 mm y la mediana ma = 85 mm.
Lado a = 60mm, la altura ha = 50mm y la diferencia de los ángulos B y C (
Determinar un triángulo conocido un lado, la altura y la mediana correspondientes a dicho lado.
Lado a = 100 mm, la altura ha = 80 mm y la mediana ma = 85 mm.
88.-
Determinar un triángulo conocida la mediana y la altura correspondientes
a un lado y uno de los otros dos lado.
Mediana ma = 75 mm, la altura ha = 70mm y lado c = 80 mm.
Determinar un triángulo conocida la mediana y la altura correspondientes a un lado y uno de sus ángulos.
Mediana ma = 75 mm, la altura ha = 70mm y ángulo B (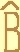 )
= 60º.
)
= 60º.
Mediana ma = 75 mm, la altura ha = 70mm y lado c = 80 mm.
Determinar un triángulo conocida la mediana y la altura correspondientes a un lado y uno de sus ángulos.
Mediana ma = 75 mm, la altura ha = 70mm y ángulo B (
89.-
Determinar un triángulo conocida la suma de dos lados (a+b), la diferencia
de otros dos lados (b-c) y uno de los ángulos ( Â ).
a+b = 80 mm, b-c = -20 mm y  = 50º.
Determinar un triángulo conocida la suma de dos lados (a+b), el tercer lado (c) y el ángulo opuesto a éste lado ( ).
).
a+b = 90 mm, c = 40 mm y = 50º.
= 50º.
a+b = 80 mm, b-c = -20 mm y  = 50º.
Determinar un triángulo conocida la suma de dos lados (a+b), el tercer lado (c) y el ángulo opuesto a éste lado (
a+b = 90 mm, c = 40 mm y
90.-
Determinar un triángulo conocida la suma de dos lados (a+b), la diferencia
de otros dos lados (b-c) y uno de los ángulos (  ).
).
a+b = 133 mm, b-c = 21 mm y = 45º. Solución
1
= 45º. Solución
1
Determinar un triángulo conocida la suma de dos lados (a+b), la diferencia de otros dos lados (b-c) y uno de los ángulos ( ).
).
a+b = 133 mm, b-c = 21 mm y = 45º. Solución
2
= 45º. Solución
2
a+b = 133 mm, b-c = 21 mm y
Determinar un triángulo conocida la suma de dos lados (a+b), la diferencia de otros dos lados (b-c) y uno de los ángulos (
a+b = 133 mm, b-c = 21 mm y
91.-
Determinar las circunferencias tangentes a la recta r y que pasan por
los puntos P y Q. Método Potencia.
Obtener las circunferencias tangentes a las rectas r y s que pasan por el punto P. Método Potencia.
Obtener las circunferencias tangentes a las rectas r y s que pasan por el punto P. Método Potencia.
92.-
Rectas tangentes a una elipse desde un punto exterior P. Método de la
circunferencia principal.
Trazar las rectas tangentes a una hipérbola equilátera desde el punto P. Método de la circunferencia principal.
Distancia focal = 75 mm.
Trazar las rectas tangentes a una hipérbola equilátera desde el punto P. Método de la circunferencia principal.
Distancia focal = 75 mm.
93.-
Determinar un triángulo conocido el Circuncentro (O), el Baricentro (G)
y un vértice (A).
Determinar un triángulo conocido el Circuncentro (O), el lado b, definido por los vértices (A y C) y la mediana mc = 75 mm.
Obtener las dos soluciones.
Determinar un triángulo conocido el Circuncentro (O), el lado b, definido por los vértices (A y C) y la mediana mc = 75 mm.
Obtener las dos soluciones.
94.-
Determinar las circunferencias tangentes a la circunferencia dada, que
pasan por el punto P y tienen su centro sobre la curva C dada .
(Seis soluciones)
Determinar las circunferencias tangentes a la recta dada, que pasan por el punto P y tienen su centro sobre la curva C dada .
(Cuatro soluciones)
(Seis soluciones)
Determinar las circunferencias tangentes a la recta dada, que pasan por el punto P y tienen su centro sobre la curva C dada .
(Cuatro soluciones)
95.-
Determinar los puntos del plano desde los cuales se ven tres segmentos
contiguos, alineados, bajo el mismo ángulo.
AB = 4cm, BC = 2cm, CD = 3cm.
(Dos soluciones)
AB = 4cm, BC = 2cm, CD = 3cm.
(Dos soluciones)
96.-
Determinar el lugar geométrico de los puntos del plano cuya suma de distancias
a dos rectas ( r, s ) es constante.
Pr + Ps = K = 25mm
Determinar el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos rectas ( r, s ) es constante.
Pr - Ps = K = 15mm
Pr + Ps = K = 25mm
Determinar el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos rectas ( r, s ) es constante.
Pr - Ps = K = 15mm
97.-
Determinar un triángulo conocidos los radios de las circunferencias exinscritas
ra =3 cm, rb = 3,5 cm y
rc = 4 cm.
98.-
Determinar un triángulo conocido el perímetro 2p = 200 mm, el radio de
la circunferencia exinscrita ra = 40 mm
y el lado a =60 mm.
Determinar un triángulo conocido el semiperímetro menos un lado p - a = 50 mm, el radio de la circunferencia inscrita
r = 27 mm y el lado b = 80 mm.
y el lado a =60 mm.
Determinar un triángulo conocido el semiperímetro menos un lado p - a = 50 mm, el radio de la circunferencia inscrita
r = 27 mm y el lado b = 80 mm.
99.-
Determinar un triángulo conocidos los lados b = 90mm, c = 58 mm y la bisectriz
correspondiente al ángulo A Va = 63 mm.
100.-
Dividir el triángulo dado en dos partes equivalentes, según una recta
paralela a una dirección dada.
Dividir el trapecio dado en cuatro partes equivalentes, según una rectas paralelas a sus bases.
Dividir el trapecio dado en cuatro partes equivalentes, según una rectas paralelas a sus bases.
101.-
Construir un heptadecágono conocida su altura (distancia desde un vértice
a su lado opuesto). Altura h = 80mm
Sin utilizar homotecia o semejanza. Método directo.
Sin utilizar homotecia o semejanza. Método directo.
102.-
Construir un cuadrilátero inscriptible conocido el radio de la circunferencia
circunscrita R = 80mm, sus dos diagonales
d1 = 120mm d2 = 130mm y el ángulo que forman éstas a = 90º.
d1 = 120mm d2 = 130mm y el ángulo que forman éstas a = 90º.
103.-
Determinar un triángulo rectángulo conocida la suma de la hipotenusa y
el cateto menor (a + c) = 130 mm y el radio de
la circunferencia inscrita r = 15 mm.
Determinar un triángulo conocido el lado a = 70 mm, el ángulo opuesto  = 65º y el punto P que dista 40 mm del
vértice B y 54 mm de C. El punto P pertenece a la bisectriz del ángulo A.
la circunferencia inscrita r = 15 mm.
Determinar un triángulo conocido el lado a = 70 mm, el ángulo opuesto  = 65º y el punto P que dista 40 mm del
vértice B y 54 mm de C. El punto P pertenece a la bisectriz del ángulo A.
104.-
Determinar un triángulo conocido el radio de la circunferencia circunscrita
R = 40 mm, el radio de la circunferencia inscrita
r = 14 mm. y el ángulo C = 45º.
Determinar un triángulo conocida la diferencia entre el lado a y el lado c, (a-c)= 40 mm, el ángulo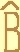 = 45º y el lado
b = 70 mm.
= 45º y el lado
b = 70 mm.
r = 14 mm. y el ángulo C = 45º.
Determinar un triángulo conocida la diferencia entre el lado a y el lado c, (a-c)= 40 mm, el ángulo
105.-
Determinar un triángulo rectángulo ( Â = 90º), conocido el lado b = 75
mm y la diferencia entre los lados a y c (a-c) = 40 mm.
Determinar un triángulo rectángulo ( Â = 90º), conocido el perímetro 2p= 120 mm y la altura ha = 22,5 mm.
Determinar un triángulo rectángulo ( Â = 90º), conocido el perímetro 2p= 120 mm y la altura ha = 22,5 mm.
106.-
Construir un triángulo, conocidos los puntos ( M, N, P) que son los puntos
de intersección de las bisectrices con la circunferencia
circunscrita.
Construir un triángulo, conocida la altura y la mediana correspondientes al vértice A, ha = 55 mm, ma = 60mm. El triángulo es
isósceles a = b.
circunscrita.
Construir un triángulo, conocida la altura y la mediana correspondientes al vértice A, ha = 55 mm, ma = 60mm. El triángulo es
isósceles a = b.
107.-
Construir un triángulo, conocida la altura, la bisectriz y el ángulo correspondiente
al vértice A.
ha = 65mm, Va = 70mm y  = 75º
Construir un triángulo, conocidas las alturas correspondientes a dos lados y la mediana correspondiente al tercer lado.
ha = 60mm, hb = 65mm y mc = 70 mm
ha = 65mm, Va = 70mm y  = 75º
Construir un triángulo, conocidas las alturas correspondientes a dos lados y la mediana correspondiente al tercer lado.
ha = 60mm, hb = 65mm y mc = 70 mm
108.-
Construir un triángulo, conocido un lado el radio de la circunferencia
inscrita y un ángulo no opuesto al lado.
a = 65mm, r = 20mm y = 60º
= 60º
Construir un triángulo, conocida la altura correspondiente a un lado la mediana correspondiente a otro lado y un ángulo.
ha = 45mm, mb = 60mm y Â= 75º
a = 65mm, r = 20mm y
Construir un triángulo, conocida la altura correspondiente a un lado la mediana correspondiente a otro lado y un ángulo.
ha = 45mm, mb = 60mm y Â= 75º
109.-
Construir un triángulo, conocido el perímetro 2p = 240 mm, el radio de
la circunferencia exinscrita rb = 40 mm y el ángulo  = 75º.
Construir un triángulo, conocido un lado a = 100 mm, la altura correspondiente al lado ha = 60 mm y el ángulo que forma la
mediana mb con otro lado c-mb = 45º.
Construir un triángulo, conocido un lado a = 100 mm, la altura correspondiente al lado ha = 60 mm y el ángulo que forma la
mediana mb con otro lado c-mb = 45º.
110.-
Determinar los elementos, básicos, de una homología que transformen el
cuadrilátero ABCD en un cuadrado de 50 mm de lado.
111.-
Determinar las tangentes interiores y exteriores a dos elipses definidas
por sus ejes reales. Posteriormente trazar las elipses.
112.-
Obtener, gráficamente el resultado de 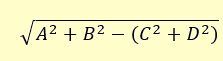
A = 70 mm, B = 50 mm, C = 40 mm y D = 60 mm
Obtener, gráficamente el resultado de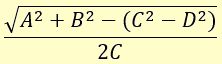
A = 70 mm, B = 50 mm, C = 40 mm y D = 60 mm
A = 70 mm, B = 50 mm, C = 40 mm y D = 60 mm
Obtener, gráficamente el resultado de
A = 70 mm, B = 50 mm, C = 40 mm y D = 60 mm
113.-
Construir un triángulo conocidos los siguientes elementos: a = 80mm, hb
= 55mm y hc = 65mm.
Inscribir en un triángulo dado DEF un triángulo ABC cuyos lados son paralelos a los lados de otro triángulo dado GHI.
Inscribir en un triángulo dado DEF un triángulo ABC cuyos lados son paralelos a los lados de otro triángulo dado GHI.
114.-
Construir un triángulo conocidos los siguientes elementos: a = 60mm, b
+ c = 95mm y el ángulo  = 75º.
Construir un triángulo conocidos los siguientes elementos: a = 70mm, b - c = 25mm y el ángulo  = 75º.
Construir un triángulo conocidos los siguientes elementos: a = 70mm, b - c = 25mm y el ángulo  = 75º.
115.-
Construir un triángulo conocidos los siguientes elementos: Radio de la
circunferencia inscrita r = 17,5 mm, Ángulo  = 30º y
Radio de la circunferencia exinscrita ra = 35 mm.
Construir un triángulo conocidos los siguientes elementos: ma = 83 mm, ha = 75 mm y radio de la circunferencia inscrita r = 22mm.
Radio de la circunferencia exinscrita ra = 35 mm.
Construir un triángulo conocidos los siguientes elementos: ma = 83 mm, ha = 75 mm y radio de la circunferencia inscrita r = 22mm.
116.-
Construir un triángulo conocidos los siguientes elementos: el lado c =
75 mm, la altura correspondiente al lado hc = 50 mm y
la diferencia de los ángulo A y B, Â - = 55º
= 55º
Construir un triángulo conocidos los siguientes elementos: Lado a = 75 mm, la suma de los lados b + c = 105 mm y el ángulo  = 85º.
la diferencia de los ángulo A y B, Â -
Construir un triángulo conocidos los siguientes elementos: Lado a = 75 mm, la suma de los lados b + c = 105 mm y el ángulo  = 85º.
D1 = 45 mm y D2 = 62 mm.
119.-
Construir un triángulo conocidos los siguientes elementos: el lado b =
85 mm, el lado c= 100 mm y la bisectriz correspondiente al
ángulo Â, Va = 90mm.
Construir un triángulo conocidos los siguientes elementos: el lado a = 70 mm, el ángulo  = 40º y la bisectriz Va = 85 mm.
ángulo Â, Va = 90mm.
Construir un triángulo conocidos los siguientes elementos: el lado a = 70 mm, el ángulo  = 40º y la bisectriz Va = 85 mm.
120.-
Construir un triángulo conocidos los siguientes elementos: el lado a =
72 mm, la suma de los lados b + c = 108 mm y la diferencia de
los ángulos C y B, -
- 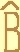 =
20º.
=
20º.
Construir un triángulo conocidos los siguientes elementos: el lado a = 72 mm, la diferencia de los lados c - b = 20 mm y la diferencia de
los ángulos C y B, -
- 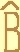 =
20º.
=
20º.
los ángulos C y B,
Construir un triángulo conocidos los siguientes elementos: el lado a = 72 mm, la diferencia de los lados c - b = 20 mm y la diferencia de
los ángulos C y B,
121.-
Construir un triángulo conocidos los siguientes elementos: las medianas
mb = 75 m, mc = 84 mm y
el ángulo  = 50º.
= 50º.
Construir un triángulo conocidos los siguientes elementos: el lado a = 72 mm, la diferencia de los lados b - c = 20 mm y el ángulo  = 75º.
Construir un triángulo conocidos los siguientes elementos: el lado a = 72 mm, la diferencia de los lados b - c = 20 mm y el ángulo  = 75º.
122.-
Construir un triángulo conocidos los siguientes elementos:
la altura ha = 60 mm y los lados b = 75 mm y c = 65 mm.
Construir un triángulo conocidos los siguientes elementos:
el lado a = 70 mm, la diferencia de los lados b y c, b - c = 20 mm y el ángulo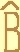 = 60º.
= 60º.
Construir un triángulo conocidos los siguientes elementos: el lado a = 72 mm, la altura ha = 40 mm y la relación entre los lados b / c = 2.
2 Soluciones
la altura ha = 60 mm y los lados b = 75 mm y c = 65 mm.
Construir un triángulo conocidos los siguientes elementos:
el lado a = 70 mm, la diferencia de los lados b y c, b - c = 20 mm y el ángulo
Construir un triángulo conocidos los siguientes elementos: el lado a = 72 mm, la altura ha = 40 mm y la relación entre los lados b / c = 2.
2 Soluciones
123.-
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 20 mm, el lado a = 75 mm y la diferencia de los lados b y c, b - c = 15 mm.
Construir un triángulo conocidos los siguientes elementos:
el lado a = 52 mm, la altura ha = 28 mm y la suma de los cuadrados de los lados b y c, b2 + c2 = K2 = 5120.
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 10 mm, el lado c = 70 mm y la suma de los lados a y b, a + b = 100 mm.
el radio de la circunferencia inscrita r = 20 mm, el lado a = 75 mm y la diferencia de los lados b y c, b - c = 15 mm.
Construir un triángulo conocidos los siguientes elementos:
el lado a = 52 mm, la altura ha = 28 mm y la suma de los cuadrados de los lados b y c, b2 + c2 = K2 = 5120.
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 10 mm, el lado c = 70 mm y la suma de los lados a y b, a + b = 100 mm.
124.-
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 15 mm, la altura ha= 75 mm y la mediana ma = 90 mm.
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 25 mm, la altura ha = 60 mm y la diferencia de los ángulos B y C,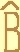 -
-  = 25º.
= 25º.
el radio de la circunferencia inscrita r = 15 mm, la altura ha= 75 mm y la mediana ma = 90 mm.
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 25 mm, la altura ha = 60 mm y la diferencia de los ángulos B y C,
125.-
Construir un triángulo conocidos los siguientes elementos:
el radio de la circunferencia inscrita r = 15 mm, la altura ha = 75 mm y la diferencia entre los lados b y c, b - c = 20 mm.
Construir un triángulo conocidos los siguientes elementos:
Rectángulo en A, la suma de la hipotenusa y un cateto a + c = 130 mm y el radio de la circunferencia inscrita r = 15 mm.
2 Soluciones
el radio de la circunferencia inscrita r = 15 mm, la altura ha = 75 mm y la diferencia entre los lados b y c, b - c = 20 mm.
Construir un triángulo conocidos los siguientes elementos:
Rectángulo en A, la suma de la hipotenusa y un cateto a + c = 130 mm y el radio de la circunferencia inscrita r = 15 mm.
2 Soluciones
126.-
Construir un cuadrilátero inscriptible conocidos los siguientes elementos:
el radio de la circunferencia circunscrita R = 50 mm, la
diagonal AC = 90 mm, la diagonal BD = 95 mm y la suma de los lados AB y AD, AB + AD = 150mm.
Construir un cuadrilátero inscriptible conocidos los siguientes elementos: el radio de la circunferencia circunscrita R = 45 mm, la
diagonal AC = 80 mm, la diagonal BD = 90 mm y la suma de los lados AB y AD, AB - AD = 30mm.
diagonal AC = 90 mm, la diagonal BD = 95 mm y la suma de los lados AB y AD, AB + AD = 150mm.
Construir un cuadrilátero inscriptible conocidos los siguientes elementos: el radio de la circunferencia circunscrita R = 45 mm, la
diagonal AC = 80 mm, la diagonal BD = 90 mm y la suma de los lados AB y AD, AB - AD = 30mm.
127.-
Construir un triángulo conocidos los siguientes elementos: el lado a =
70 mm, el lado b = 60 mm y el ángulo que forma la mediana mc
con el lado c (AMcC) = 75º. Siendo Mc el pie de la mediana mc.
Construir un triángulo conocidos los siguientes elementos: el lado a = 50 mm, el ángulo  = 85º y la suma de el lado b y el doble
del lado c, b + 2c = 110 mm.
2 Soluciones
con el lado c (AMcC) = 75º. Siendo Mc el pie de la mediana mc.
Construir un triángulo conocidos los siguientes elementos: el lado a = 50 mm, el ángulo  = 85º y la suma de el lado b y el doble
del lado c, b + 2c = 110 mm.
2 Soluciones
128.-
Construir un triángulo conocidos los siguientes elementos: el lado a =
60 mm, el ángulo  = 75º y la suma de el lado b y el lado c
b + c = 95 mm.
Construir un triángulo conocidos los siguientes elementos: el ángulo  = 45º, el ángulo = 65º y la suma de los
lados a y b
= 65º y la suma de los
lados a y b
a + b = 80 mm.
Construir un triángulo conocidos los siguientes elementos: el ángulo  = 45º, el ángulo = 65º y la suma de los
lados a y c
= 65º y la suma de los
lados a y c
a + c= 80 mm.
b + c = 95 mm.
Construir un triángulo conocidos los siguientes elementos: el ángulo  = 45º, el ángulo
a + b = 80 mm.
Construir un triángulo conocidos los siguientes elementos: el ángulo  = 45º, el ángulo
a + c= 80 mm.
129.-
Construir un triángulo conocidos los siguientes elementos: el radio de
la circunferencia circunscrita R = 70 mm, el radio de la
cincunferencia inscrita r = 30 mm y el ángulo  = 45º.
cincunferencia inscrita r = 30 mm y el ángulo  = 45º.
130.-
Construir un triángulo conocidos los siguientes elementos: el radio de
la circunferencia exinscrita ra = 40 mm, la mediana
ma = 50 mm y el ángulo  = 45º.
Construir un triángulo conocidos los siguientes elementos: la bisectriz wa = 56 mm, la diferencia de los lados b y c, b-c = 45 mm
y el ángulo  = 65º.
ma = 50 mm y el ángulo  = 45º.
Construir un triángulo conocidos los siguientes elementos: la bisectriz wa = 56 mm, la diferencia de los lados b y c, b-c = 45 mm
y el ángulo  = 65º.
131.-
Construir un triángulo conocidos los siguientes elementos: la bisectriz
wa = 66 mm, el producto de los lados b y c b.c = 4950 mm2
y el ángulo  = 70º.
Construir un triángulo conocidos los siguientes elementos: la diferencia de los lados a y b, a - b = 48 mm, la diferencia de los lados
b y c , c - b = 40 mm y el ángulo  = 80º.
y el ángulo  = 70º.
Construir un triángulo conocidos los siguientes elementos: la diferencia de los lados a y b, a - b = 48 mm, la diferencia de los lados
b y c , c - b = 40 mm y el ángulo  = 80º.
132.-
Realizar la figura siguiente, resolviendo los diferentes trazados de tangencias
que se presentan. Dejar los trazados auxiliares.
Indicar, claramente, los centros y puntos de tangencia.
Indicar, claramente, los centros y puntos de tangencia.
133.-
Construir un cuadrilátero incriptible conocidos los cuatro lados a = 45
mm, b = 45 mm, c = 60 mm y d = 75 mm.
Construir un cuadrilátero conocidos los siguientes elementos: la suma de los lados a y d, a + d = 100 mm, la suma de los lados
b y c, b + c = 130mm y los ángulos a = 100º, b = 110º y g = 75º.
Construir un cuadrilátero conocidos los siguientes elementos: la suma de los lados a y d, a + d = 100 mm, la suma de los lados
b y c, b + c = 130mm y los ángulos a = 100º, b = 110º y g = 75º.
134.-
Construir un triángulo conocidas las distancias del Ortocentro a los vértices.
OA = 85 mm, OB = 35 mm y OC = 45 mm.. (Siendo O el Ortocentro).
OA = 85 mm, OB = 35 mm y OC = 45 mm.. (Siendo O el Ortocentro).
135.-
Construir un triángulo conocidos los siguientes elementos: Radio de la
circunferencia inscrita r = 20 mm, Ángulo  = 45º y
el lado a = 75 mm.
Construir un triángulo conocidos los siguientes elementos: el vértice A se encuentra en el punto superior de la intersección de las
circunferencias dadas. Los vértices B y C, están uno sobre cada una de las circunferencias dadas. El ángulo B = 45º y el ángulo C = 30º.
Dos soluciones
el lado a = 75 mm.
Construir un triángulo conocidos los siguientes elementos: el vértice A se encuentra en el punto superior de la intersección de las
circunferencias dadas. Los vértices B y C, están uno sobre cada una de las circunferencias dadas. El ángulo B = 45º y el ángulo C = 30º.
Dos soluciones
136.-
Dibujar la figura dada a escala 1 : 1. Solucionar todos los casos de tangencias
necesarios.
137.-
Determinar un triángulo isósceles conocida la altura correspondiente a
un lado igual hb = 80 mm y el radio de la circunferencia
inscrita r = 30 mm.
Determinar una circunferencia que pase por los puntos A y B, conocidos, y que corte a la recta r según un segmento de magnitud
igual a 50 mm.
inscrita r = 30 mm.
Determinar una circunferencia que pase por los puntos A y B, conocidos, y que corte a la recta r según un segmento de magnitud
igual a 50 mm.
138.-
Inscribir en el triángulo dado un rectángulo de superficie igual a 10
cm²
2 Soluciones.
2 Soluciones.
139.-
Dado el triángulo equilátero ABC, obtener el Lugar Geometrico de los puntos
del plano que cumplan la siguiente condición
PA = PB + PC.
PA = PB + PC.
140.-
Dado el triángulo ABC dividirlo, mediante una recta r secante, a los lados
a y b, de manera que quede dividido en un triángulo y
un cuadrilátero de igual superficie. El cuadrilátero será inscriptible. Obtener el radio de la circunferencia circunscrita al cuadrilátero.
un cuadrilátero de igual superficie. El cuadrilátero será inscriptible. Obtener el radio de la circunferencia circunscrita al cuadrilátero.
141.-
Obtener un punto interior P, de un triángulo ABC, tal que al unir dicho
punto con los vértices quede
el triángulo dividido en tres triángulos equivalentes.
Trazar las circunferencias de radio 27 mm, que sean tangentes a la de centro O y que corten a la de
centro O´ según una cuerda de 39 mm.
2 Soluciones
el triángulo dividido en tres triángulos equivalentes.
Trazar las circunferencias de radio 27 mm, que sean tangentes a la de centro O y que corten a la de
centro O´ según una cuerda de 39 mm.
2 Soluciones
142.-
Determinar las circunferencias que tienen el mismo eje radical que las
de centro en O´ y O´´ y son
tangentes a la de centro en O.
2 Soluciones
tangentes a la de centro en O.
2 Soluciones
r = 20 mm, Ángulo C = 60º y el lado c = 80 mm.
Resolver analítica y geométricamente.
de la circunferencia circunscrita R = 65 mm y el lado c = 80 mm.
Construir un triángulo conocidos los siguientes elementos: El Ortocentro (H), el Circuncentro (O) y el punto
medio (M) del lado AB.
en otro triángulo y un trapezoide de igual área.
Construir un triángulo conocidos los siguientes elementos: El lado (a = 35 mm), el radio de la circunferencia circunscrita
(R = 25 mm) y la bisectriz del ángulo A (Wa = 40 mm).
Determinar el lugar geométrico de los puntos cuya suma de distancias a dos rectas r y s es constante e igual a 35mm.
Determinar el lugar geométrico de los puntos cuya diferencia de cuadrados a dos puntos fijos es constante e igual a 124mm.
Realizar un par de casos con circunferencias de comprobación.
los lados a y c es de 30º.
Determinar un cuadrilátero conociendo las diagonales d1 = 80mm y d2 = 70mm, su ángulo 125º y dos ángulos
opuestos 120º y 70º.
Determinar un cuadrilátero conociendo tres lados a = 60mm, b = 30mm, c = 85 mm y los ángulos adyacentes
al cuarto lado 70º y 90º
una diagonal con el lado = 30º
Determinar un cuadrilátero conociendo sus diagonales D1 = 100mm, D2 = 80mm, el ángulo que forman a = 120º, la relación
entre los lados CD/BC = 5/2 y el ángulo que forman los otro dos lados b = 75º
 Descargar archivo de datos
Descargar archivo de datos Determinar un cuadrilátero conociendo los lados AB = 85, CD = 50mm y los ángulos BAC ( a ) = 40º, ACD ( b ) = 20º y el
ángulo BDA ( g ) = 80º
Obtener las dos soluciones
 Descargar archivo de datos
Descargar archivo de datos CD =70mm.
Determinar un cuadrilátero conociendo las diagonales D1 = 110mm, D2 = 90mm, el ángulo que forman las diagonales ( g ) = 120º y
los ángulos BCA ( a ) = 70º y DAC ( b ) = 30º
 Descargar archivo de datos
Descargar archivo de datos lado correspondiente a = 75º.
Determinar un triángulo conocido el ángulo  = 60º, la suma de los lados a+b = 60mm y la suma de los lados a+c = 70mm.
 Descargar archivo de datos
Descargar archivo de datos  Descargar archivo de datos
Descargar archivo de datos ángulos B - C = 25º.
Determinar un triángulo conocido el ángulo  = 60º, la bisectriz Wa = 40mm y el perímetro a + b + c = 150mm
 Descargar archivo de datos
Descargar archivo de datos los cuales el lado b queda dividido por hb; AHb - CHb = 64mm.
Dados tres puntos A, B, C y una recta r, que pasa por A. Describir una circunferencia que pase por A y por B y corte a la recta r en
un punto D tal que CD sea tangente a la circunferencia.
 Descargar archivo de datos
Descargar archivo de datos ángulos B - C = 40º.
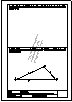
Dado el triángulo ABC trazar una recta r, paralela a BC, de manera que XY = BX + CY. Los puntos X e Y son los de corte de la
recta r con los lados c y b.
 Descargar archivo de datos
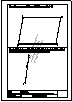
Descargar archivo de datos En un triángulo ABC se da AB en magnitrud y posición; además el ángulo  = 70º y el punto D, donde el diámetro del círculo
circunscrito que pasa por C corta a AB; se pide construir el círculo circunscrito y el triángulo.
 Descargar archivo de datos
Descargar archivo de datos  Descargar archivo de datos
Descargar archivo de datos  Descargar archivo de datos
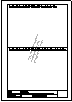
Descargar archivo de datos Determinar un triángulo, conocido el ángulo  = 60º, el radio de la circunferencia inscrita r = 12 mm y el perímetro 2p = 170mm.
 Descargar archivo de datos
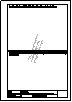
Descargar archivo de datos Determinar un triángulo conocido el radio de la circunferencia inscrita r = 10mm, el radio de la circunferencia exinscrita ra = 25mm y la
bisectriz Wa = 45mm.
 Descargar archivo de datos
Descargar archivo de datos Determinar un triángulo conocida la altura ha = 45mm y las medianas ma = 60mm y mb = 72 mm.
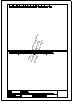 Descargar archivo de datos
Descargar archivo de datos Determinar un triángulo conocida la altura ha = 60mm y las medianas mb = 57mm y mc = 75 mm.
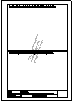 Descargar archivo de datos
Descargar archivo de datos Determinar un triángulo conocida la altura ha = 60mm; la mediana ma = 70mm y la relación hc : b = 5 : 6.
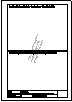 Descargar archivo de datos
Descargar archivo de datos Determinar un triángulo conocida la mediana ma = 40mm; la mediana mc = 44mm y el ángulo que forma
la mediana mb con el lado a = 20º.
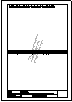 Descargar archivo de datos
Descargar archivo de datos Determinar un triángulo conocidas las alturas ha = 60mm; la altura hb = 85mm y el ángulo que forma
la mediana ma con el lado b = 40º.
 Descargar archivo de datos
Descargar archivo de datos mb con el lado c = 25º.
Determinar un triángulo conocidas las altura ha = 40mm; la suma de los lados b y c; b + c = 120mm y la
relación entre las alturas hb y hc hb / hc = 7 / 4. .
 Descargar archivo de datos
Descargar archivo de datos línea EF que une los puntos medios de los lados AB y CD que mide 68 mm.
Construir un rectángulo, conocido el lado mayor (el que pasa por B y por D), mide 80 mm.
Cada lado pasa por uno de los puntos, ABCD , dados.
 Descargar archivo de datos
Descargar archivo de datos una longitud dada = 63 mm y que AX : CY = 5 : 3
Trazar una recta de dirección dada que corte a dos circunferencias dadas, de tal manera que las cuerdas
interceptadas tengan una suma de 60 mm.
Dos Soluciones
 Descargar archivo de datos
Descargar archivo de datos Construir un trapecio conociéndose las diagonales, d1 = 60 mm y d2 = 85 mm, la línea que une los puntos medios de
los lados no paralelos EF = 65 mm y el ángulo a = 75º.
 Descargar archivo de datos
Descargar archivo de datos a = 135º y la suma de los lados contiguos AD + DC = 130 mm.
Construir un trapecio conociéndose las diagonales, d1 = 65 mm y d2 = 75 mm, el ángulo que forman las diagonales
a = 125º y la diferencia de los lados contiguos AD - DC = 45 mm.
 Descargar archivo de datos
Descargar archivo de datos área = 1925 mm 2
Circunscribir a un triángulo dado ABC, el mayor triángulo equilátero posible.
 Descargar archivo de datos
Descargar archivo de datos Resolver analítica y geométricamente.
 Descargar archivo de datos
Descargar archivo de datos d2 = 100 mm y el ángulo que forman 110º.
Construir un cuadrilátero circunscriptible conociendo AD = 75 mm, AB = 55 mm el ángulo D = 80º y el ángulo B = 120º
 Descargar archivo de datos
Descargar archivo de datos X e Y son los puntos de corte de la recta con los lados AB y BC.
 Descargar archivo de datos
Descargar archivo de datos CD = 60 mm y el ángulo que forman estos lados 50º.
 Descargar archivo de datos
Descargar archivo de datos diferencia entre las bases B - b = 25 mm.
Construir un trapecio conociendo las diagonales d1 = 100 mm ; d2 = 110 mm, la línea que une los puntos
medios de las diagonales MN y la línea que une los puntos medios de dos lados opuestos PQ.
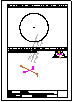 Descargar archivo de datos
Descargar archivo de datos A y B (Â -
Construir un triángulo del cual se conoce el lado a = 64 mm ; la altura ha = 52 mm y la diferencia entre
los ángulos B y C (
 Descargar archivo de datos
Descargar archivo de datos diferencia entre los ángulos B y C (B - C) = 30º.
 Descargar archivo de datos
Descargar archivo de datos las bases B + b = 180 mm.
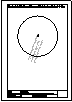 Descargar archivo de datos
Descargar archivo de datos AB = 30 mm; BC = 50 mm; CD = 70 mm y DA = 60 mm.
En una circunferencia inscribir un triángulo conociendo los puntos medios de los arcos que subtienden las lados.
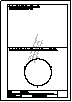 Descargar archivo de datos
Descargar archivo de datos Construir un triángulo conociendo el ángulo  = 60º, la suma de los lados a + c = 110 mm y la suma
de los lados a + b = 100 mm.
 Descargar archivo de datos
Descargar archivo de datos sobre los cuatro lados.
 Descargar archivo de datos
Descargar archivo de datos Trazar por O una recta que corte a las paralelas en X y en Y de tal manera que AX + BY (tomadas cada
una con su signo) sea igual a una longitud dada. AX (+); BY(-); L = 30 mm.
Por un punto P, dado, trazar una recta que determine en un ángulo dado un triángulo de perímetro
dado 2p = 200 mm.
 Descargar archivo de datos
Descargar archivo de datos mediana ma = 70mm.
Construir un triángulo conocidos los siguientes datos: el ángulo  = 60º, el radio de la circunferencia
inscrita r = 15 mm y la diferencia entre los lados b y c; c - b = 20 mm.
 Descargar archivo de datos
Descargar archivo de datos 4 Soluciones
 Descargar archivo de datos
Descargar archivo de datos Desde un barco se ven dos puntos conocidos bajo un ángulo dado 45º; el barco avanza una longitud dada según
una dirección dada, y se ven los mismos puntos bajo un ángulo de 100º; se pide determinar la posición del barco.
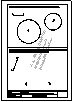 Descargar archivo de datos
Descargar archivo de datos tangencia en la recta.
Resolver por dilataciones.
Determinar las circunferencias tangentes a una circunferencia dada y a una recta dada conocido el punto de
tangencia en la recta.
Resolver por inversión.
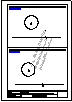 Descargar archivo de datos
Descargar archivo de datos una de ellas.
Resolver por dilataciones.
Determinar las circunferencias tangentes a dos circunferencias dadas conocido el punto de tangencia en
una de ellas.
Resolver por inversión.
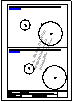 Descargar archivo de datos
Descargar archivo de datos circunferencia inscrita r = 15 mm.
Construir un triángulo isósceles conocidas la altura ha = 60 mm y la mediana ma = 65 mm
correspondientes a uno de los lados iguales.
 Descargar archivo de datos
Descargar archivo de datos y BDA = 65º.
En un triángulo se traza una línea que une el vértice con un punto de la base. Hallar sobre esta recta un
punto desde donde se vean los dos segmentos, m y n, de la base bajo ángulos iguales.
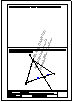 Descargar archivo de datos
Descargar archivo de datos y la relación BC : CD = 2.
Sobre una recta r, dada, hallar un punto P que equidiste de un punto dado A, en la misma recta r y de
otra recta dada s.
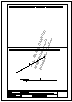 Descargar archivo de datos
Descargar archivo de datos de los otros dos b + d = 95 mm y el radio de la circunferencia circunscrita R = 37,5 mm.
 Descargar archivo de datos
Descargar archivo de datos otros dos en dos circunferencias, también dadas.
Dos soluciones
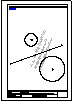 Descargar archivo de datos
Descargar archivo de datos proporcional entre BC y CD.
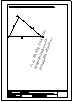 Descargar archivo de datos
Descargar archivo de datos
proyecciones de B y C estén en una relación dada (AB) : (BC) = 2 : 3.
Trazar las tangentes comunes a dos circunferencias.
 Descargar archivo de datos
Descargar archivo de datos
dos tangentes sean paralelas y que sus distancias a O estén en una relación dada m : n = 3 : 2.
 Descargar archivo de datos
Descargar archivo de datos