| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2023 (Ordinaria) |
|
Enunciado
|
DATOS
|
SOLUCIONES
|
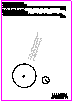
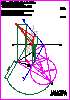
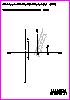
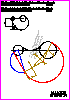
1. Dadas dos circunferencias de centros O1 y O2 :
- Determine el eje radical de ambas circunferencias (1 p.).
- Obtenga el único punto A del eje radical desde el que se observa
el segmento O1 O2 bajo un ángulo de 45º y que cabe en los límites
del papel (1 p.).
|
|
|
2. Dibuje a escala 4:7 el trazado de las tangencias del croquis (1,6 p.).
Indique los centros de los arcos y los puntos de tangencia. No borre
las operaciones auxiliares que permitan determinarlos.
Se valorará el uso de la escala gráfica (0,4 p.).
|
|
|
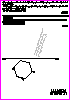
3. De una parábola conocemos el foco F, y dos puntos, P y Q, situados
a un mismo lado del eje de dicha parábola:
- Determine la directriz (0,8 p.)
- Determine el eje (0,3 p.)
- Determine el vértice V (0,2 p.)
- Obtenga dos puntos más de la parábola, situados a diferente
lado del eje que los puntos P y Q (0,4 p.)
- Dibuje la parábola (0,3 p.)
|
|
|
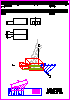
4. Represente a escala 1:1 la figura dibujada en el croquis
adjunto, determinando los centros y los puntos de tangencia.
Deje indicadas las líneas auxiliares de construcción necesarias
para obtener la solución (2 PUNTOS).
|
|
|
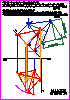
5. Dados la proyección horizontal del triángulo ABC y los
vértices B y C abatidos:
- Obtenga la proyección vertical del triángulo (1,4 p.).
- Determine las proyecciones del circuncentro del
triángulo (1,6 p.)
|
|
|
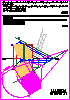
6. Represente un prisma recto de altura 40 mm situado en el
primer diedro, cuya base es el hexágono regular representado
contenido en el plano horizontal de proyección (0,6 p.).
Determine las proyecciones de la sección producida al
prisma por el plano definido por los puntos A, B y C, estando
A y B situados en el plano horizontal de proyección y C en la
base superior del prisma (1,4 p.).
Determine la verdadera magnitud de la sección (1 p.).
|
|
|
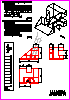
7. Dado el sólido representado en dibujo isométrico (sin coeficientes
de reducción) a escala 1 : 1:
- Dibuje a escala 7 : 8, en sistema diédrico europeo, el alzado, la
planta y la vista lateral izquierda, con todas las líneas ocultas
(1,8 p.). Utilice como alzado la vista según A. Tome las medidas
directamente de la figura. Se valorará la obtención de la escala
gráfica y el uso de la misma (0,2 p.).
- Acote las vistas según las normas (1 p.).
|
|
|
8. Dadas la planta y la vista lateral derecha de una pieza
representadas a escala 1:1 en el sistema diédrico europeo:
- Represente el alzado delineado con todas sus )
aristas ocultas (1 p.).
- Acote completamente la pieza según las normas (1 p.)
- Represente en croquis (a mano alzada) una vista
axonométrica de la pieza (1 p.). Se valorará el dibujo de las
aristas ocultas necesarias para mostrar la forma de todas
las partes de la pieza.
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD JuLio 2023 (ExtraOrdinaria) |
|
Enunciado |
DATOS
|
SOLUCIONES
|
1. Represente el triángulo
ABC sabiendo que el ángulo en el vértice C
es
de 60º, el lado BC mide 60 mm y el vértice C está lo más alejado
posible
de la recta r (1 p.)
Dados el eje
de afinidad (recta r) y el punto A´ afín del punto A,
obtenga
el triángulo afín del ABC (1 p.).
|
|
|
2. Represente a escala
1 : 1 la figura dibujada en el croquis adjunto,
determinando
los centros y puntos de tangencia. Deje indicadas
las
líneas auxiliares de construcción necesarias para obtener la
solución.
Situe el centro O1 en la posición indicada.
|
|
|
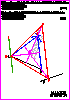
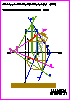
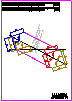
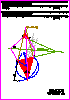
3. Tres campamentos
están asentados en los puntos A, B , C:
-
Determine el punto de reunión, X, para que la distancia recorrida
en
línea recta desde los tres campamentos hasta dicho punto X sea
la
misma (0,4 p.).
- Determine
el punto de reunión, Y, para que se cumpla
simultáneamente
(0,4 p.)
o La distancia
recorrida en línea recta desde los campamentos A y C
hasta
dicho punto Y sea la misma.
o
La distancia recorrida desde el campamento B hasta dicho punto Y
sea
la menor posible.
- Determine
el punto de observación, Z, (todas la soluciones posibles),
desde
el que se cumpla simultáneamente (1,2 p.)
o
Los campamentos A y C se observen bajo un ángulo de 30º.
o
Los campamentos B y C se observen bajo un ángulo de 45º. |
|
|
4. Represente a escala
4 : 9 la figura dibujada en el croquis adjunto,
determinando
los centros y los puntos de tangencia. Deje indicadas
las
líneas auxiliares de construcción necesarias para obtener la
solución.
Situe el centro O1 en la posición indicada. Se valorará
la obtención de la escala gráfica y
el uso de la misma. (2 PUNTOS) |
|
|
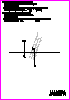
5. Dadas las proyecciones
de la recta r y del punto A:
-
Represente las trazas del plano a determinado
por la recta r y el
punto
A (1 p.).
- Representa
las trazas del plano b que pasa por el punto
A y es
perpendicular
a la recta r (1 p.).
-
Obtenga la intersección entre los planos a y
b (1 p.). |
|
|
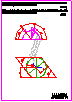
6. Dado el plano a,
las proyecciones del punto A y la proyección
vertical
del punto B:
- Obtenga las proyecciones del
triángulo equilátero ABC, de lado
70
mm, contenido en el plano a y situado en el primer
diédro (1,6 p.).
- Siendo el triángulo ABC la
cara de un tetraedro regular, obtenga las
proyecciones
del tetraedro sabiendo que está por encima del plano a
(1,4 p.). |
|
|
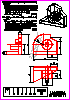
7. Dado el sólido representado en dibujo isométrico (sin coeficientes
de reducción), a escala 1 :1 :
- Dibuje a escala 5 : 4, en sistema diédrico europeo, el alzado, la planta
y la vista lateral derecha, con todas sus líneas ocultas ( 1,8 p.).
Utilice como alzado la vista según "A". Tome las medidas directamente
de la figura. Se valorará la obtención de la escala gráfica y el uso de la
misma (0,2 p.).
- Acote las vistas según las normas (1 p.).
|
|
|
8. Dados el alzado y la planta de una pieza, con todas sus caras planas,
representados a escala 2:3 en el sistema diédrico europeo:
- Represente la vista lateral izquierda delineada con todas sus
aristas ocultas (1 p.)
- Acote completamente la pieza según las normas (1 p.)
- Represente en croquis (a mano alzada) una vista axonométrica de
la pieza (1 p.). Se valorará el dibujo de aristas ocultas necesarias
para mostrar la forma de todas las partes de la pieza.(1 p.).
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Junio 2024 (Ordinaria) |
|
Enunciado |
DATOS
|
SOLUCIONES
|
1. Dibuje un rombo sabiendo que uno de los ángulos entre sus lados
es de 52,5° y que el radio de la circunferencia inscrita es de 30 mm.
Obtenga el ángulo de 52,5° con el compás. Deje indicadas todas las
líneas auxiliares de construcción.
|
|
|
2. Dado el segmento AB, construya el triángulo equilátero ABC con el
vértice C lo más alto posible (0,3 p.). Halle el homólogo de ABC (1,2 p.)
sabiendo que:
- el centro del triángulo es el centro de homología O,
- la paralela a BC desde el vértice A es el eje de homología E
- el homólogo de B está contenido en la recta r dada.
|
|
|
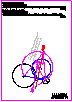
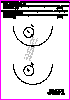
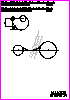
3. Determine la circunferencia de centro O3 tangente a la circunferencia
de centro O1y a la semicircunferencia de centro O2 conociendo el
punto de tangencia T.
El centro O3 está situado a la derecha de O1 . (0,9 p.)
Determine la circunferencia de radio 18 mm y centro O6 tangente a la
circunferencia de centro O4 y a la semicircunferencia de centro O5 .
El centro O6 está situado a la derecha de O4. (0,6 p.).
|
|
|
4. De una hipérbola se conoce el foco F1 , el eje, un punto P de la curva
y la tangente en dicho punto tp. Obtenga:
- El otro foco F2 (0,5 p.)
- Los vértices (0,6 p.)
- Las asíntotas (0,4 p.)
- Deje indicadas todas las líneas auxiliares de construcción (1,5 PUNTOS)
|
|
|
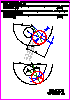
5. Dada la pirámide recta de base triangular ABC y vértice V, dibuje
las proyecciones (1,2 p.) y la verdadera magnitud (0,8 p.) de la
sección que le produce el plano a.
|
|
|
6. Determine las proyecciones de la distancia del punto P al plano
definido por los puntos A, B y C. (2 PUNTOS)
|
|
|
7. a) Obtenga las proyecciones del cuadrado ABCD (1 p.) sabiendo que:
- está contenido en un plano a perpendicular al Plano Vertical de
Proyección
- está situado en el primer diedro
b) Siendo el cuadrado ABCD la cara de un hexaedro regular, obtenga
las proyecciones del hexaedro sabiendo que está situado por encima
del plano a . (1 p.) (2 PUNTOS)
|
|
|
8. Dados el alzado, la planta y la vista lateral de una pieza, represente
la vista directa de la misma en sistema axonométrico oblicuo
(perspectiva caballera), a la misma escala que las vistas sabiendo que
el coeficiente de reducción es CR= 0,7 . Represente también las líneas
ocultas. Se valorará el uso de la escala gráfica para aplicar la reducción.
(2 PUNTOS)
|
|
|
9. Dada la pieza representada a escala 1:1 en dibujo isométrico
(sin coeficientes de reducción):
- Dibuje en croquis (a mano alzada) en sistema diédrico europeo, el
alzado, la planta y la vista lateral derecha, con todas sus líneas
ocultas (2 p.). Utilice como alzado la vista según A.
- Acote las vistas según las normas (1 p.). (3 PUNTOS)
|
|
|
10. Dados el alzado y el perfil izquierdo de una pieza simétrica
representados a escala 2:1, en sistema diédrico europeo, se pide:
- Represente la planta delineada con todas sus aristas ocultas (1 p.).
- Represente en croquis (a mano alzada) una vista axonométrica de
la pieza (1 p.). Se valorará el dibujo de aristas ocultas necesarias
para mostrar la forma de todas las partes de la pieza.
- Acote completamente la pieza según norma (1 p.). (3 PUNTOS)
|
|
|
| EVALUACIÓN
DEL BACHILLERATO PARA EL ACCESO A LA UNIVERSIDAD Julio 2024 (Extraordinaria) |
|
Enunciado |
DATOS
|
SOLUCIONES
|
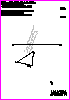
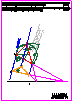
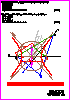
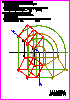
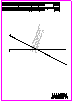
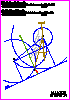
1. Dadas las rectas r y s, represente todos los segmentos de longitud 40 mm
que se apoyen en las dos rectas y que formen 45° con la recta r.
No borre las construcciones auxiliares y utilice la notación adecuada
para entender el procedimiento. (1,5PUNTOS)
|
|
|
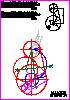
2. Complete, a escala 1:1, el trazado de tangencias de la figura.
Indique los centros de los arcos y los puntos de tangencia.
No borre las operaciones auxiliares que permitan determinarlos.
(1,5 PUNTOS)
|
|
|
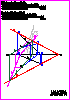
3. Represente un triángulo ABC en el que el ángulo en C sea de 45° y la
longitud AC de 60 mm. De todas las soluciones posibles elija aquella
en la que el punto C está lo más cerca posible del borde inferior, del
papel (0,6 p.).
Dados los puntos A’-B’-D’ homólogos de A, B y D respectivamente,
determine el centro y el eje de la homología (0,6 p.). Obtenga el
triángulo homólogo de ABC (0,3 p.). (1,5 PUNTOS)
|
|
|
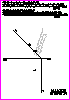
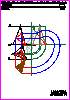
4. Dados el foco F y los puntos A y B de una parábola,
- Obtenga la directriz, eje y vértice V de la parábola.
Seleccione la directriz que se encuentre por debajo del foco (0,8 p.).
- Obtenga la tangente a la parábola en el punto A (0,7 p.). (1,5 PUNTOS)
|
|
|
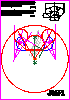
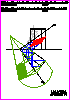
5. Dado el prisma recto de base rectangular y el plano 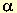 dado por sus dado por sus
trazas obtenga la sección producida por el plano al prisma en
proyecciones (1,2 p.) y en verdadera magnitud (0,8 p.). (2 PUNTOS)
|
|
|
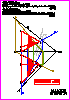
6. Dada la pirámide VABC y el plano 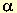 , ,
a) Analice la visibilidad de la pirámide y represéntela (0,4 p.).
b) Dibuje las proyecciones de la sección que el plano 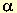 produce en la produce en la
pirámide, analizando también su visibilidad (1,6 p.). (2 PUNTOS)
|
|
|
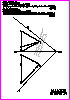
7. Obtenga la intersección de los tres planos 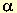 , ,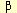 y y 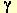 . (2 PUNTOS) . (2 PUNTOS)
|
|
|
8. Dados el alzado, la planta y la vista lateral de una pieza, represente
la vista directa de la misma en dibujo isométrico (sin coeficientes de
reducción), a la misma escala que las vistas. Sitúe el punto O en la
posición indicada. Incluya todas las líneas ocultas. (2 PUNTOS)
|
|
|
9. Dada la pieza representada a escala 1:1 en dibujo isométrico
(sin coeficientes de reducción):
- Dibuje en croquis (a mano alzada) en sistema diédrico europeo, el
alzado, la planta y la vista lateral izquierda, con todas sus líneas
ocultas (2 p.). Utilice como alzado la vista según A.
- Acote las vistas según las normas (1 p.). (3 PUNTOS)
|
|
|
10. Dados el alzado y la planta de una pieza representados a
escala 2:3 en el sistema diédrico europeo:
- Represente la vista lateral derecha delineada con todas sus aristas
ocultas (1 p.).
- Acote completamente la pieza según las normas (1 p.).
- Represente en croquis (a mano alzada) una vista axonométrica de
la pieza (1 p.). Se valorará el dibujo de las aristas ocultas necesarias
para mostrar la forma de todas las partes de la pieza. (3 PUNTOS)
|
|
|





























 dado por sus
dado por sus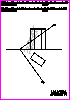
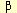 y
y 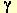 . (2 PUNTOS)
. (2 PUNTOS)